Question

[Ngọc Mai]

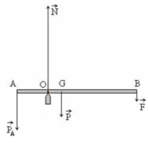
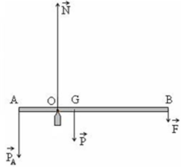
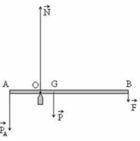
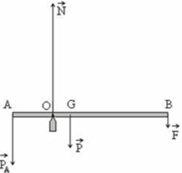
1 thanh gỗ AB dài 40cm, khối lượng 150g. Treo thanh nằm ngang bởi 2 lực kế thẳng đứng tại 2 đầu A, B. Biết rằng lực kế ở đầu B chỉ 0,6 N.

a. Hỏi trọng tâm của thanh nằm ở vị trí nào?

b. Lực kế ở đầu A chỉ bao nhiêu?

c. Di chuyển điểm đặt của 1 trong 2 lực kế 1 đoạn x, khi đó số chỉ lực kế có giá trị gấp 2 lần nhau. Tính x.

Answer 1

[Mysterious Person]

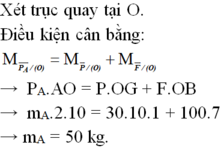
trường hợp này mình lấy \(g=10m\backslash s^2\) cho dể tính nha

tóm tắt đề bài : \(\left\{{}\begin{matrix}l=40cm=0,4m\\m=150g=0,15kg=1,5N\\vịtrícủatrọngtâm\\F_A=?\end{matrix}\right.\) trong đó \(F_A\) là lực mà lực kế ở đầu A chỉ đặt tương tự để B có lực \(F_B=0,6N\)

(làm câu b xong mới tính được câu a chứ bạn)

b) ta có \(P=F_A+F_B\Leftrightarrow F_A=P-F_B=1,5-0,6=0,9\left(N\right)\)

vậy lực kế ở đầu A chỉ \(0,9\left(N\right)\)

a) từ đề ta có : \(\left\{{}\begin{matrix}F_A.r_A=F_B.r_B\\r_A+r_B=0,4\end{matrix}\right.\) (\(r_A;r_B\) lần lược là khoảng cách từ trọng tâm đến \(A;B\) )

\(\Leftrightarrow\left\{{}\begin{matrix}0,9r_A=0,6r_B\\r_A+r_B=0,4\end{matrix}\right.\) giải ra ta được \(\left\{{}\begin{matrix}r_A=0,16\\r_B=0,24\end{matrix}\right.\)

vậy trọng tâm cách đầu A \(0,16m\) và cách đầu B \(0,24m\)

c) nếu di chuyển ở đầu A thì ta có : \(2F_Ar_x=F_Ar_A\Leftrightarrow r_x=\dfrac{F_Ar_A}{2F_A}=\dfrac{r_A}{2}=\dfrac{0,16}{2}=0,08m\)

vậy \(r_x\) cách trọng tâm \(0,08m\) \(\) \(\Rightarrow\) nó đã di chuyển lên 1 đoạn bằng \(0,16-0,08=0,08m\)

trường hợp này \(x=0,08m\)

nếu di chuyển ở đầu B thì ta có : \(2F_Br_x=F_Br_B\Leftrightarrow r_x=\dfrac{F_Br_B}{2F_B}=\dfrac{r_B}{2}=\dfrac{0,24}{2}=0,12m\)

vậy \(r_x\) cách trọng tâm \(0,12m\) \(\) \(\Rightarrow\) nó đã di chuyển lên 1 đoạn bằng \(0,24-0,12=0,12m\)

trường hợp này \(x=0,12m\)

vậy \(x\) có 2 giá trị là \(x=0,08;x=0,12\)

Answer 2

[TU MIG]

cho hỏi 2 lực kế có giá trị gấp 2 lần nhau là j v??