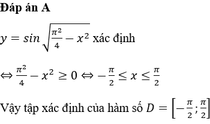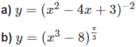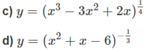K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HN
0
Những câu hỏi liên quan
26 tháng 1 2022
b: A(1;1) B(-2;4)
\(M\left(x;x^2\right)\)
Theo đề, ta có: MA=MB
\(\Leftrightarrow\sqrt{\left(x-1\right)^2+\left(x^2-1\right)^2}=\sqrt{\left(x+2\right)^2+\left(x^2-4\right)^2}\)
\(\Leftrightarrow x^2-2x+1+x^4-2x^2+1=x^2+4x+4+x^4-8x^2+16\)
\(\Leftrightarrow6x^2-6x-18=0\)
\(\Leftrightarrow x^2-x-3=0\)
\(\Delta=\left(-1\right)^2-4\cdot1\cdot\left(-3\right)=13>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-\sqrt{13}}{2}\\x_2=\dfrac{1+\sqrt{13}}{2}\end{matrix}\right.\)
Vậy: \(M\left(\dfrac{1-\sqrt{13}}{2};\dfrac{7-\sqrt{13}}{2}\right);M\left(\dfrac{1+\sqrt{13}}{2};\dfrac{7+\sqrt{13}}{2}\right)\)
CM
1 tháng 7 2018
a. Định nghĩa 1 : (Hàm số sin): Quy tắc tương ứng với mỗi số thực x với số thực sinx.
sin: R -> R
x -> y = sinx.
Hàm số y = sinx có tập xác định là R, tập giá trị là đoạn [-1;1].
b.Định nghĩa 2 : (Hàm số cosin): Quy tắc tương ứng với mỗi số thực x với số thực cosx.
cos : R -> R
x -> y = cosx.
Hàm số y = cosx có tập xác định là R, tập giá trị là đoạn [-1;1]
c. Định nghĩa 3: (Hàm số tang): Hàm số tang là hàm số được xác định bởi công thức
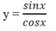
tan : D -> R
x -> y = tanx.
Hàm số y = tanx có tập xác định: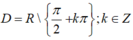 
Tập giá trị của hàm số y = tanx là R.
d. Định nghĩa 4 : (Hàm số cotang): là hàm số được xác định bởi công thức
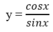
cot : D -> R
x -> y = cotx.
Hàm số y = cotx có tập xác định D = {x ∈ R \ x ≠ kπ, k ∈ Z}. Tập giá trị của hàm số y = cotx là tập R.
PT
1
PT
1
CM
30 tháng 9 2018
Hàm số xác định khi x 2 + x – 6 > 0 hay x < -3 và x > 2.
Vậy tập xác định là (− ∞ ; −3) ∪ (2; + ∞ ).
28 tháng 2 2022
Bài 1:
a: Thay x=2 và y=1 vào y=ax, ta được: 2a=1
hay a=1/2
Vậy: f(x)=1/2x
b: f(-2)=1/2x(-2)=-1
f(4)=1/2x4=2
f(0)=0
PT
1
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
CM
24 tháng 12 2018
a) Hàm số xác định khi x 2 − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.
Vậy tập xác định của hàm số đã cho là R \ {1;3}.
b) Hàm số xác định khi x 3 – 8 > 0 hay x > 2. Vậy tập xác định là (2; + ∞ ).
c) Hàm số xác định khi x 3 – 3 x 2 + 2x > 0 hay x(x – 1)(x – 2) > 0