Tính góc lớn nhất của tam giác ABC biết :
a) Các cạnh a = 3cm, b = 4cm và c = 6cm
b) Các cạnh a = 40cm, b = 13cm và c = 37cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét: Trong một tam giác, góc đối diện với cạnh lớn nhất là góc lớn nhất.
a) Cạnh c = 6cm lớn nhất nên góc lớn nhất là góc C:
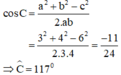
Vậy góc lớn nhất là 117º.
b) Cạnh a = 40cm lớn nhất suy ra góc lớn nhất là góc A:
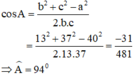
Vậy góc lớn nhất bằng 94º

Ta biết trong tam giác thì đối diện với cạnh lớn nhất là góc lớn nhất, vậy trong câu a) góc lớn nhất là góc C còn trong câu b) góc lớn nhất là góc A
a) cos =
=
≈ -0,4583 =>
= 117016’
b)cos =
=
=>
= 93041’


a: AH=căn 13^2-5^2=12cm
CH=12^2/5=28,8cm
BC=28,8+5=33,8cm
AC=căn 28,8*33,8=31,2cm
b: AH=căn 3*4=2căn 3(cm)
AB=căn 3*7=căn 21(cm)
AC=căn 4*7=2căn 7(cm)
c: CH=4^2/3=16/3cm
AB=căn 4^2+3^2=5cm
AC=căn 16/3*25/3=20/3(cm)

Câu 1 : Góc lớn nhất là góc A ( đáp án đúng là a )
Câu 2 : Cạnh lớn nhất là cạnh AC ( đáp án đúng là b )
Câu 3 : Trong tam giác, điểm cách đều 3 cạnh là giao điểm của ba đường phân giác ( đáp án đúng là đáp án c )
Câu 4 : Chu vi tam giác đó là 22cm ( đáp án đúng là đáp án c )
Câu 5 : Bộ ba đoạn thẳng không thể là ba cạnh của một tam giác là 3cm,2cm,6cm ( đáp án đúng là đáp án b )
Câu 6 : Khi đó ta có MP>NP>MN ( đáp án đúng là đáp án c )
Câu 7 : Trọng tâm của tam giác là giao điểm của ba đường trung tuyến ( đáp án đúng là đáp án a )

ΔABC~ΔA'B'C'
=>\(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
=>\(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\)
=>AB là cạnh nhỏ nhất trong ΔABC
Theo đề, ta có: AB=3cm
=>\(\dfrac{AC}{4}=\dfrac{BC}{5}=\dfrac{3}{3}=1\)
=>\(AC=4\cdot1=4\left(cm\right);BC=5\cdot1=5\left(cm\right)\)
Ta biết trong tam giác thì đối diện với cạnh lớn nhất là góc lớn nhất, vậy trong câu a) góc lớn nhất là góc C còn trong câu b) góc lớn nhất là góc A
a) cos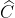 =
= 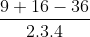 =
= 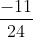 ≈ -0,4583 =>
≈ -0,4583 => 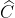 = 117016’
= 117016’
b)cos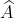 =
=  =
= 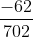 =>
=> 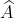 = 93041’
= 93041’