Tìm p/số dương \(\dfrac{a}{b}\) tối giản nhỏ nhất sao cho khi nhân \(\dfrac{a}{b}\)lần lượt với các p/số \(\dfrac{36}{5};\dfrac{24}{7};\dfrac{16}{3}\) đều cho ra kết quả là số nguyên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2018
Gọi a là số nguyên dương cần tìm
Để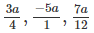 
là những số nguyên thì a phải chia hết cho 4, cho 11, cho 12; a là số nguyên dương nhỏ nhất nên a là BCNN(4,11,12) = 132.
21 tháng 3 2017
TQ: Phân số a/b nhỏ nhất mak khi nhân x/y;z/t;m/n đc số nguyên thì :
a là BCNN ( y,n,t )
b là ƯCLN ( x,z,m )
=> a/b= 105/4
Chúc bạn học giỏi
4 tháng 3 2018
khi nhân \(\frac{a}{b}\)với các ps \(\frac{36}{5};\frac{24}{7};\frac{16}{3}\)đều đc số nguyên nên
a\(⋮\)3;5;7 và 36;24;16 \(⋮\)b
a/b nhỏ nhất => a là BCNN(3;5;7) và b là ƯCLN(36;24;16)
=> a=105 ; b=4 (t\m a/b tối giản)
k biết đúng k
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 2 2019
\(P=\dfrac{16}{x}+\dfrac{\dfrac{1}{4}}{y}=\dfrac{4^2}{x}+\dfrac{\left(\dfrac{1}{2}\right)^2}{y}\ge\dfrac{\left(4+\dfrac{1}{2}\right)^2}{x+y}=\dfrac{81}{20}\)
\(\Rightarrow P_{min}=\dfrac{81}{20}\) khi \(\left\{{}\begin{matrix}x=\dfrac{40}{9}\\y=\dfrac{5}{9}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=81\\b=20\end{matrix}\right.\) \(\Rightarrow a+b=101\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2021
\(y=\dfrac{4}{x}+\dfrac{9}{1-x}\ge\dfrac{\left(2+3\right)^2}{x+1-x}=25\)
Dấu "=" xảy ra khi \(\dfrac{x}{2}=\dfrac{1-x}{3}\Rightarrow x=\dfrac{2}{5}\)
\(\Rightarrow a+b=7\)
H9
HT.Phong (9A5)
CTVHS
10 tháng 10 2023
a) Các phân số tối giản là: \(\dfrac{1}{5};\dfrac{7}{6};\dfrac{9}{19}\)
b) Ba phân số tối giản là: \(\dfrac{3}{2};\dfrac{5}{6};\dfrac{4}{9}\)
Ba phân số chưa tối giản là:
\(\dfrac{10}{18}=\dfrac{10:2}{18:2}=\dfrac{5}{9}\)
\(\dfrac{20}{50}=\dfrac{20:10}{50:10}=\dfrac{2}{5}\)
\(\dfrac{3}{12}=\dfrac{3:3}{12:3}=\dfrac{1}{4}\)