K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

21 tháng 3 2017
TQ: Phân số a/b nhỏ nhất mak khi nhân x/y;z/t;m/n đc số nguyên thì :
a là BCNN ( y,n,t )
b là ƯCLN ( x,z,m )
=> a/b= 105/4
Chúc bạn học giỏi

4 tháng 3 2018
khi nhân \(\frac{a}{b}\)với các ps \(\frac{36}{5};\frac{24}{7};\frac{16}{3}\)đều đc số nguyên nên
a\(⋮\)3;5;7 và 36;24;16 \(⋮\)b
a/b nhỏ nhất => a là BCNN(3;5;7) và b là ƯCLN(36;24;16)
=> a=105 ; b=4 (t\m a/b tối giản)
k biết đúng k

13 tháng 4 2018
Gọi a là số nguyên dương cần tìm
Để 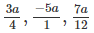

13 tháng 4 2018
Từ 
ab = 8a(b – a)
ab = 8ab – 8a2
8a2 = 7ab
8a = 7b hay