giải phương trình
x3 +10y3=25z3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
18 tháng 8 2019
b) x 3 - 3 x 2 + 2 = 0
⇔ x 3 - x 2 - 2 x 2 + 2 = 0
⇔ x 2 (x - 1) - 2( x 2 - 1) = 0
⇔ (x - 1)[ x 2 - 2(x + 1)] = 0
⇔ (x - 1)( x 2 - 2x - 2) = 0
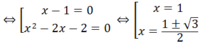
Vậy phương trình đã cho có tập nghiệm là S = {1; (1 ± 3 )/2}
CM
7 tháng 9 2019
x3 + 3x2 – 2x – 6 = 0
⇔ (x3 + 3x2) – (2x + 6) = 0
⇔ x2(x + 3) – 2(x + 3) = 0
⇔ (x2 – 2)(x + 3) = 0
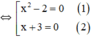
+ Giải (1): x2 – 2 = 0 ⇔ x2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
CM
26 tháng 11 2018
x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
CM
31 tháng 3 2018
x 3 + 3 x 2 + 2 x = 0 ⇔ x ( x 2 + 3 x + 2 ) = 0
⇔ x = 0 hoặc x 2 + 3 x + 2 = 0 ( 1 )
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
PT
1
CM
24 tháng 4 2017
Ta có: x 3 – 5 x 2 –x +5 = 0 ⇔ x 2 ( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
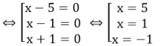
Vậy phương trình đã cho có 3 nghiệm :x1 = 5;x2 =1;x3=-1
CM
28 tháng 9 2019
Ta có: 3 x 3 +6 x 2 -4x =0 ⇔ x(3 x 2 +6x -4) =0
⇔ x = 0 hoặc 3 x 2 +6x -4 =0
Giải phương trình 3 x 2 +6x -4 =0
∆ ’ = 3 2 - 3(-4) = 9 + 12 = 21 > 0
∆ ' = 21
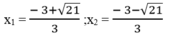
Vậy phương trình đã cho có 3 nghiệm
CM
23 tháng 4 2017
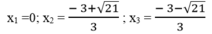
Ta có: 2 x 2 + 3 2 -10 x 3 -15x =0 ⇔ 2 x 2 + 3 2 - 5x(2 x 2 +3)=0
⇔ (2 x 2 +3)( 2 x 2 +3 - 5x) = 0 ⇔ (2 x 2 +3)( 2 x 2 - 5x +3)=0
Vì 2 x 2 ≥ 0 nên 2 x 2 +3 > 0
Suy ra : 2x2 - 5x +3=0
∆ = - 5 2 -4.2.3 =25 -24=1 > 0
∆ = 1 = 1
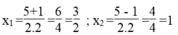
vậy phương trình đã cho có 2 nghiệm: x1 = 3/2 ; x2 = 1
CM
5 tháng 8 2019
a) x 3 – 8 = 0
⇔ (x − 2)( x 2 + 2x + 4) = 0
⇔ x1 = 2; x2 = −1 + i 3 ; x2 = −1 - i 3
b) x 3 + 8 = 0
⇔ (x + 2)( x 2 − 2x + 4) = 0
⇔ x1 = −2; x2 = 1 + i 3 ; x3 = 1 - i 3
ta có : x3 +10y3=25z3 (1)
vì 25z3 \(⋮\)5 \(\Leftrightarrow\) x3 + 10y3 \(⋮\) 5. mà 10y3 \(⋮\) 5 \(\Rightarrow\) x3 \(⋮\)5. hay x \(⋮\) 5
-đặt x=5x1.thay vào (1)\(\Rightarrow\)125x13 + 10y3 = 25z3 \(\Rightarrow\) 25x13 + 2y3= 5z3 (2) y \(⋮\) 5.
- đặt y = 5y1 thay vào (2)\(\Rightarrow\) 25x13+250y13=5z3\(\Rightarrow\) 5x13 + 50y13=z3 (3)\(\Rightarrow\)z\(⋮\)5
- đặt z=5z1 thay vào (3)\(\Rightarrow\)5x13 +50y13=125z13\(\Rightarrow\) x13+10y13= 25z13.
nếu (x;y;z) là nghiệm của (1) thì ( x1;y1;z1 ) cùng là nghiệm của (1) hay (\(\dfrac{x}{5}\); \(\dfrac{y}{5};\dfrac{z}{5}\)) là nghiệm của (1) tổng quát ta có : (\(\dfrac{x}{5^x};\dfrac{y}{5^x};\dfrac{z}{5^x}\)) là nghiệm của (1)
với mọi giá trị của x \(\in\) N* điều xảy ra \(\Leftrightarrow\)x = y = z = 0
nhận định x = y = z = 0
Nè làm giùm đi Akai Haruma , ngonhuminh ,