Giải dùm mình câu a, b, c, d, e,f với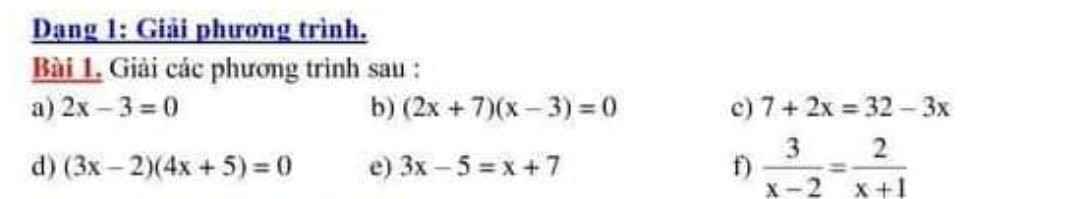

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


B A F N D M C E
Cô hướng dẫn em câu d nhé, theo cô thấy thì đề của em không đúng, góc vuông ở đây là BND nhé ^^
Do F đối xứng với E qua A nên tam giác BEF cân tại B, từ đó góc FBA = góc ABE. Lại do câu b, góc ABE = góc AMD nên góc NBD bằng góc NMD. Vậy tứ giác BMDN nội tiếp.
Ta thấy góc BMD vuông nên BD là đường kính. Từ đó góc DNB vuông (đpcm)
Chúc em học tốt :))))



a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE và \(\widehat{ABD}=\widehat{AED}=90^0\)
hay DE\(\perp\)AC
c: Xét ΔDBF vuông tại B và ΔDEC vuông tại E có
DB=DE
BF=EC
Do đó: ΔDBF=ΔDEC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
hay F,D,E thẳng hàng

a: Xét ΔADB và ΔADE có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE và \(\widehat{ABD}=\widehat{AED}=90^0\)
hay DE\(\perp\)AC
c: Xét ΔBDF vuông tại B và ΔEDC vuông tại E có
DB=DE
BF=EC
Do đó: ΔBDF=ΔEDC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
hay F,D,E thẳng hàng


a: Ta có: \(2x-3=0\)
\(\Leftrightarrow2x=3\)
hay \(x=\dfrac{3}{2}\)
b: Ta có: \(\left(2x+7\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+7=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=3\end{matrix}\right.\)
c: Ta có: \(2x+7=32-3x\)
\(\Leftrightarrow5x=25\)
hay x=5
d: Ta có: \(\left(3x-2\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
e: Ta có: \(3x-5=x+7\)
\(\Leftrightarrow2x=12\)
hay x=6
f: Ta có: \(\dfrac{3}{x-2}=\dfrac{2}{x+1}\)
Suy ra: \(3x+3=2x-4\)
\(\Leftrightarrow x=-7\left(nhận\right)\)