Cho hình vuông ABCD có AC cắt BD tại O. Gọi M là điểm bất kì thuộc cạnh BC ( M \(\ne\) B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh tam giác OME vuông cân
b) Chứng minh ME song song với BN.
c) Từ C, kẻ \(CH\perp BN\left(H\in BN\right)\). CMR : 3 điểm O, M, H thẳng hàng
(giúp mình câu c là chính...
Đọc tiếp
Cho hình vuông ABCD có AC cắt BD tại O. Gọi M là điểm bất kì thuộc cạnh BC ( M \(\ne\) B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh tam giác OME vuông cân
b) Chứng minh ME song song với BN.
c) Từ C, kẻ \(CH\perp BN\left(H\in BN\right)\). CMR : 3 điểm O, M, H thẳng hàng
(giúp mình câu c là chính nha)
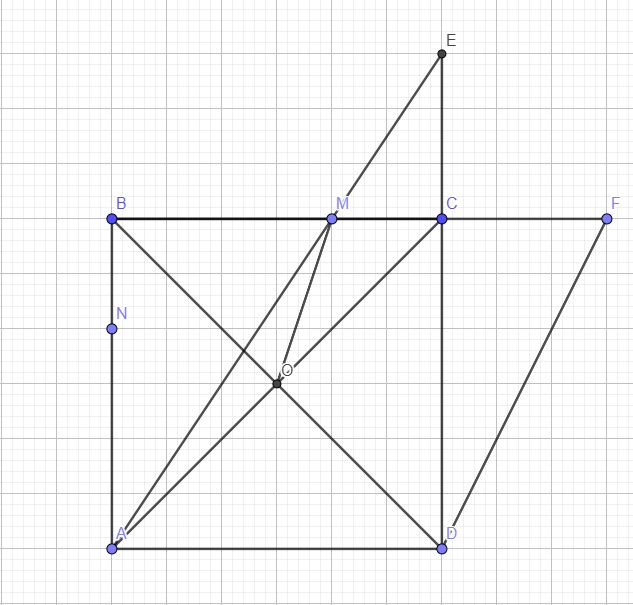
a) và b) thì dễ rồi nhé !!!
c)
Gọi giao điểm của OM và BN là H'
Ta có : \(\widehat{MH'B}=\widehat{EMO}=45^0\)
Xét \(\Delta BMH'\) và \(\Delta OCM\) có :
\(\widehat{H}=\widehat{C}\left(=45^0\right)\)
\(\widehat{BMH'}=\widehat{CMO}\) ( đối đỉnh )
=> \(\Delta BMH'\)~ \(\Delta OMC\) ( g . g )
Ta có tỉ số :
\(\dfrac{BM}{MH'}=\dfrac{OM}{MC}\)
Lại xét \(\Delta BMO\) và \(\Delta H'MC\) có :
\(\dfrac{BM}{MH'}=\dfrac{OM}{MC}\)
\(\widehat{BMO}=\widehat{H'MC}\) ( đối đỉnh )
=> \(\Delta BMO\)~\(\Delta H'MC\) ( c . g . c )
=> \(\widehat{OBM}=\widehat{CH'M}=45^0\)
=> \(\widehat{BH'C}=90^0\)
=> H' trùng với H
=> đfcm
Để c/m 3 điểm thẳng hàng bạn chứng minh \(\widehat{OMH}\) = 180o nhé! Mik ko đủ năng lực để c/m cái này.