cho tam giác đều ABC . trên BC, CA,AB lấy 3 điểm bất kì I,J,K sao cho K khác A,B và \(\widehat{\text{IJ}K}\)= 60. chứng minh AJ. BI\(\le\)\(\frac{AB^2}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C 60 60 I K J 60 60
Ta có: \(\widehat{AKJ}+\widehat{BKI}=180^o-60^o=120^o,\widehat{BKI}+\widehat{BIK}=120^o\)
=> \(\widehat{AKJ}=\widehat{BIK}\)
Mà \(\widehat{KBI}=\widehat{JAK}\left(=60^o\right)\)
=> Tam giác KAJ đồng dạng vs tam giác IBK
=> \(\frac{BI}{AK}=\frac{BK}{AJ}\Rightarrow BI.AJ=BK.AK\le\left(\frac{BK+AK}{2}\right)^2\)=\(\frac{AB^2}{4}\)
Dấu '=" xảy ra khi và chỉ khi BK=AK hay K là trung điểm AB

Câu hỏi của marivan2016 - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo nhé!

Lấy M sao cho C là trung điểm của AM
Xét ΔABM có
K,C lần lượt là trung điểm của AB,AM
=>KC là đường trung bình của ΔABM
=>KC//BM và \(KC=\dfrac{BM}{2}\)
Xét ΔABM có
BC là đường trung tuyến
\(BJ=\dfrac{2}{3}BC\)
Do đó: J là trọng tâm của ΔABM
=>AJ cắt BM tại trung điểm của N của BM
Xét ΔABM có
K,N lần lượt là trung điểm của BA,BM
=>KN là đường trung bình của ΔABM
=>KN//AM và KN=AM/2
KN=AM/2
AC=AM/2
Do đó: KN=AC
Xét tứ giác AKNC có
NK//AC
NK=AC
Do đó: AKNC là hình bình hành
=>AN cắt KC tại trung điểm của mỗi đường
=>I là trung điểm của KC(ĐPCM)

Xét tam giác AMB và AMC có:
AB=AC (Giả thiết)
AM là cạnh chung)
MB=MC(Giả thiết)
=> tam giác AMB = tam giác AMC (c.c.c)
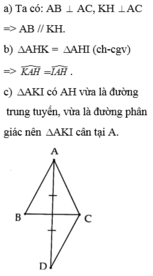
mạo phép sửa đề:\(\widehat{IKJ}=60^o\)
A B C I J K
vì tam giác ABC đều nên\(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
ta có:\(\widehat{AKJ}+\widehat{IKJ}+\widehat{IKB}=180^o\)(K\(\in\)AB)
\(\Rightarrow\widehat{AKJ}+\widehat{IKB}=180^o-\widehat{IKJ}=120^o\)(1)
xét \(\Delta BIK\):\(\widehat{B}+\widehat{IKB}+\widehat{BIK}=180^o\)(tổng 3 góc trong tam giác)
mà \(\widehat{B}=60^o\Rightarrow\widehat{BIK}+\widehat{IKB}=120^o\)(2)
từ (1)và (2):\(\widehat{AKJ}=\widehat{BIK}\)
xét \(\Delta AKJ\)và\(\Delta BIK\)có:\(\widehat{A}=\widehat{B}=60^o\left(cmt\right)\)
\(\widehat{AKJ}=\widehat{BIK}\left(cmt\right)\Rightarrow\Delta AKJ\)~\(\Delta BIK\left(g.g\right)\)
\(\rightarrow\frac{AJ}{BK}=\frac{AK}{IB}\Leftrightarrow AJ.IB=BK.AK\)
áp dụng BĐT \(\left(a+b\right)^2\ge4ab\)(cách cm:chuyển vế tương đương or dùng cauchy)\(\Rightarrow ab\le\frac{\left(a+b\right)^2}{4}\)
\(BK.AK\le\frac{\left(BK+AK\right)^2}{4}\Leftrightarrow AJ.IB\le\frac{AB^2}{4}\)
dấu = xảy ra khi BK=AK hay K là trung điểm của AB