Cho tam giác ABC cân tại A có AB < BC . Trên cạnh BC lấy hai ddieremr M và N sao cho BM = CN = AB . Chứng minh :
a ) Tam giác AMN cân.
b ) Tính số đo các góc của tam giác AMN khi góc BAC = 120 độ.
c ) Có khi nào tam giác AMN vuông cân được hay không?


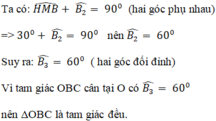
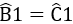
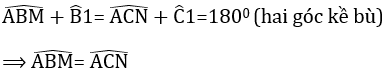
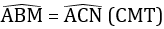
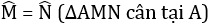

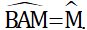
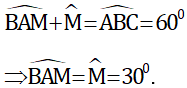
a) Vì \(\Delta\)ABC cân tại A nên AB = AC và \(\widehat{ABC}\)= \(\widehat{ACB}\)
hay \(\widehat{ABN}\) = \(\widehat{ACM}\)
Ta có: BN + NM = BM
CM + NM = CN
mà BM = CN => BN = CM
Xét \(\Delta\)ABN và \(\Delta\)ACM có:
AB = AC (c/m trên)
\(\widehat{ABN}\) = \(\widehat{ACM}\) (c/m trên)
BN = CM (c/m trên)
=> \(\Delta\)ABN = \(\Delta\)ACM (c.g.c)
=> AN = AM (2 cạnh t/ư)
Do đó \(\Delta\)AMN cân tại A
b) Áp dụng tc tổng 3 góc trong 1 tg ta có:
\(\widehat{BAC}\) + \(\widehat{ABC}\) + \(\widehat{ACB}\) = 180o
=> 120o + \(\widehat{ABC}\) + \(\widehat{ACB}\) = 180o => \(\widehat{ABC}\) + \(\widehat{ACB}\) = 60o => \(\widehat{ABC}\) = \(\widehat{ACB}\) = 30o Vì AB = BM => \(\Delta\)ABM cân tại B => \(\widehat{BAM}\) = \(\widehat{BMA}\) Áp dụng tc tổng 3 góc trong 1 tg ta có:\(\widehat{BAM}\) + \(\widehat{BMA}\) + \(\widehat{ABC}\) = 180o
=> \(\widehat{BAM}\) + \(\widehat{BMA}\) + 30o = 180o
=> \(\widehat{BAM}\) + \(\widehat{BMA}\) = 150o
=> \(\widehat{BAM}\) = \(\widehat{BMA}\) = 75o hay \(\widehat{AMN}\) = 75o
mà \(\Delta\)AMN cân tại A => \(\widehat{ANM}\) = \(\widehat{AMN}\) = 75o
Áp dụng tc tổng 3 góc trong 1 tg ta có:
\(\widehat{ANM}\) + \(\widehat{AMN}\) + \(\widehat{NAM}\) = 180o
=> 75o + 75o + \(\widehat{NAM}\) = 180o
=> \(\widehat{NAM}\) = 30o
c) \(\Delta\)AMN ko thể là tgv cân đc.
bài giải hay