Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N
Xét tam gia ABM va ANC co:
AB = AC(gt)
\(\widehat{B}\) =\(\widehat{C}\) (gt)
BM =NC (gt)
=> \(\Delta\) ABM =\(\Delta\) ANC (C.G.C)

tự kẻ hình :
a, tam giác ABC cân tại A (gt)
=> AB = AC (đn) (1)
góc ABC = góc ACB (đl)
góc ABC + góc ABM = 180 (kb)
góc ACB + góc ACN = 180 (kb)
=> góc ABM = góc ACN (2)
xét tam giác ABM và tam giác ACN có : BM = CN (gt) và (1); (2)
=> tam giác ABM = tam giác ACN (c-g-c)
=> MA = NA (đn)
=> tam giác AMN cân tại A (đn)
b, xét tam giác HBM và tam giác KCN có : MB = CN (gt)
góc M = góc N do tam giác AMN cân (câu a)
góc MHB = góc NKC = 90 do ...
=> tam giác HBM = tam giác KCN (ch - gn)
=> HB = CK (đn)
c, có AM = AN (Câu a)
AM = AH + HM
AN = AK + KN
HM = KN do tam giác HBM = tam giác KCN (câu b)
=> HM = KN

Bạn tham khảo bài này nha!
Cho Tam giác cân ABC AB=AC=10 cm,BC=16 cm.Trên đường cao AH lấy điểm I sao cho AI=1/3 AH.Kẻ tia Cx song song?
với AH, cắt tia BI tại D
a/ Tính các góc của tam giác ABC ( câu này em tìm ra được rùi làm dùm em câu b thui )
b/Tính diện tích của tứ giác ABCD
Diện tích tứ giác ABCD = diện tích tam giác ABH + diện tích tứ giác AHCD
diện tích tam giác ABH = 1/2 AH x BH
trong đó: H là trung điểm của BC (tam giác ABC cân tại A, AH là đường cao)
nên BH = 8 cm
tam giác ABH vuông tại H nên AH = căn bậc hai của ( AB x AB - BH x BH)
AH = 6cm
=> S tam giác ABH = 1/2 8 x 6 = 24cm2
- ta có IH // CD mà H là trung điểm BC => HI là đường trung bình của tam giác CBD
=> HI = 1/2 CD
mà HI = 2/3 AH = 2/3 x6 = 4
=> CD = 8cm
AH // CD => AHCD là hình thang
Diện tích hình thang AHCD = 1/2 HC x ( AH + CD) = 1/2 8 x ( 6+8)= 56 cm2
Vậy diện tích tứ giác ABCD = 24 + 56 = 80cm2

chăng co tam giac vuong can nao ma bm=cn = ab lan sau hoi bai thi hoi dang hoang
keo lam kho nguoi khac

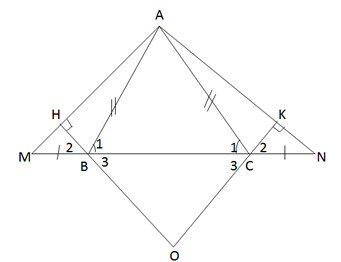
a) ∆ABC cân, suy ra ˆB1=ˆC1B1^=C1^
⇒ˆABM=ˆACN⇒ABM^=ACN^
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACNABM^=ACN^
BM = ON (gt)
Suy ra ˆM=ˆNM^=N^
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆNM^=N^ (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^
Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)
Nên ˆB3=ˆC3B3^=C3^ .
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=1800–12002=300M^=BAM^=1800–12002=300 .
Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .
Và ˆMAN=1800–(ˆAMN+ˆANM)=1800–2.300=1200MAN^=1800–(AMN^+ANM^)=1800–2.300=1200
Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.
+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)
Suy ra ˆB3=600B3^=600
Tương tự ˆC3=600C3^=600
Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).

chị tự kẻ hình :
a, xét tam giác AMB và tam giác ANC có : MB = CN (gt)
tam giác AMN cân tại A (gt) => AM = AN (đn) và góc AMN = góc ANM (tc)
=> tam giác AMB = tam giác ANC (c - g - c)
=> AB = AC (đn)
=> tam giác ABC cân tại A (đn)
b, tam giác AMB = tam giác ANC (câu a)
=> góc ABM = góc ACN (đn)
góc ABM + góc MBH = 180o (kb)
góc ACN + góc NCK = 180o (kb)
=> góc MBH = góc NCK
xét tam giác MBH và tam giác NCK có : MB = CN (gt)
góc MHB = góc CKN do MH | AB và NK | AC (gt)
=> tam giác MBH = tam giác NCK (ch - gn)
c, tam giác MBH = tam giác NCK (câu b)
=> góc BMH = góc CNK (đn)
=> tam giác MNO cân tại O (đl)
Cả Út, e lớp 4, mak biết bài lp 7, em là thần thánh ak, ns thek thôi chứ cj cx bt lm bài lớp 8 tro khi đó cj ms hok lớp 7. :))