Cho tam giác ABC vuông tại A.Gọi I là trung điểm của BC.CMR AI=1/2BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
0
24 tháng 1 2016
Mình nghĩ ra rồi! Nhưng mình ko thể vẽ hình, bạn tự vẽ nhé. Giải: K là trung điểm BC (giả thuyết) =>BK=KC. Xét tam giác ABK và tam giác ICK có: ^(góc)AKB=^CKI( đối đỉnh) AK=KI(giả thuyết) BK=KC(chứng minh trên) =>2 tam giác trên bằng nhau trường hợp cạnh-góc-cạnh =>AB=IC vì là các cạnh tương ứng. =>^BAK = ^KIC vì là các góc tương ứng. Mà 2 góc trên ở vị trí soletrong =>AB // IC => ^BAC+^ACI=180 độ vì là 2 góc trong cùng phía. Mà ^BAC=90 độ(vuông ở A) =>^ACI=90 độ => hai góc này bằng nhau. Xét tam giác ABC và tam giác ACI có: cạnh AC chung AB=CI(chứng minh trên) ^BAC=^ACI(cmt) => hai tam giác này bằng nhau trường hợp cạnh góc cạnh. b/ tam giác ABC = tam giác ACI(chứng minh trên) => AI=BC vì là các cạnh tương ứng CÓ BK+KC=BC mà BK=BC(cmt) => BK=1/2 BC CÓ AK+KI=AI mà AK=KI(gt) => AK =1/2 AI Từ 3 điều trên =>AK=BK => AK= 1/2 BC lưu ý giả thuyết là từ đề bài nhé.
8 tháng 2 2020
a) Xét \(\Delta ADB\)và \(\Delta ADC\)có:
\(AB=AC\left(gt\right)\)
\(BD=DC\)( D là trung điểm của BC )
AD là cạnh chung
\(\Rightarrow\Delta ADB=\Delta ADC\left(c.c.c\right)\)
b) Vì \(\Delta ADB=\Delta ADC\left(cmt\right)\)
\(\Rightarrow\widehat{BAD}=\widehat{CAD}\)( 2 góc tương ứng )
=> AD là tia phân giác \(\widehat{BAC}\)
c) Vì \(\Delta ADB=\Delta ADC\left(cmt\right)\)
\(\Rightarrow\widehat{D_1}=\widehat{D_2}\)( 2 góc tương ứng )
Vì \(\widehat{D_1}+\widehat{D_2}=180^0\)( 2 góc kề bù )
\(\Rightarrow\widehat{D_1}=\widehat{D_2}=\frac{180^0}{2}=90^0\)
\(\Rightarrow AD\perp BC\)
NH
8 tháng 2 2020
a , Xét Δ\(ADB\) và Δ\(ADC\) có:
\(AD\) là cạnh chung
\(A1=A2\) ( GT )
\(AB=AC\) ( GT )
⇒Δ\(ADB\)=Δ\(ADC\) ( c.g.c )
b , Vì : Δ\(ADB\)=Δ\(ADC\) ( chứng mính ý a )
⇒ \(B=C\) ( 2 góc tương ứng )
c , Vì : Δ\(ABC\) cân tại \(A\) mà \(AD\) là phân giác góc \(BAC\)
⇒ \(AD\) là đường cao ⇒ \(AD\perp BC\)
NM
0
23 tháng 3 2023
\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`IB = IC (g``t)`
`=> \text {Tam giác AIB = Tam giác AIC (c-g-c)}`
Hnhu câu `b,` bạn ghi thiếu yêu cầu rồi nhé!
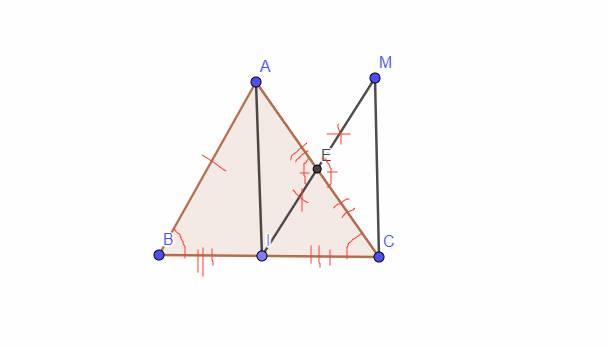
`c,` Xét Tam giác `AEI` và Tam giác `MEC` có:
`EA = EC (g``t)`
\(\widehat{AEI}=\widehat{MEC}\) `(\text {2 góc đối đỉnh})`
`EM = EI (g``t)`
`=> \text {Tam giác AEI = Tam giác MEC (c-g-c)}`
`->`\(\widehat{AIE}=\widehat{CME}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong `-> \text {AI // CM}`
Vì Tam giác `ABI =` Tam giác `ACI (a)`
`->`\(\widehat{AIB}=\widehat{AIC}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIB}+\widehat{AIC}=180^0\)
`->`\(\widehat{AIB}=\widehat{AIC}=\) `180/2=90^0`
`-> AI \bot BC`
Mà `\text {AI // CM} -> MC \bot BC`
KF
2
PT
6
DH
22 tháng 1 2017
nếu làm theo đề của Hoàng Thị Ngọc Anh thì mình làm được
Hình chắc bạn tự vẽ được
trên tia đối của tia IA lấy điểm D sao cho AI=AD
Xét tam giác AIB và tam giác DIC ta có:
AI=AD(theo cách dựng hình);
góc AIB=góc DIC(đối đỉnh)
BI=CI(gt)
do đó tam giác AIB=tam giác DIC (c.g.c)
=>AB=DC(cặp cạnh tương ứng);góc IAB=góc IDC(cặp góc tương ứng)
Vì góc IAB=góc IDC(cmt)nên AB song song DC( do có 1 cặp góc bằng nhau ở vị trí so le trong)
=>góc BAC=góc ACD=90 độ (cặp góc so le trong và góc BAC=90 độ)
Xét tam giác ABC và tam giác CDA có:
AB=CD(đã cm);
góc BAC=góc DCA(=90độ);
AC: cạnh chung
Do đó tam giác ABC = tam giác CDA (c.g.c)
=>BC=DA(cặp cạnh tương ứng)
mà AI=DI=AD/2=>AI=BC/2 (đpcm)
chúc bạn học tốt và một năm nới tốt đẹp nha!!!
Lì xì cho mình bằng cái tick nha!!!
Ta có: ΔABC vuông tại A
mà AI là đường trung tuyến
nên AI=BC/2(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)