CHO TAM GIÁC ABC CÓ 3 GÓC NHỌN, AH LÀ ĐƯỜNG CAO VÀ AH=BC. MNPQ LÀ HÌNH CHỮ NHẬT NỘI TIẾP TAM GIÁC ABC (M, N THUỘC CẠNH BC, P THUỘC AC, Q THUỘC AB). TÌM CÁCH DỰNG ĐỂ SMNPQ LỚN NHẤT VÀ CHU VI MNPQ KHÔNG ĐỔI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2018
câu hỏi của cậu giống toán lớp 9 có phải là toán lowps đâu cậu bảo
24 tháng 8 2023
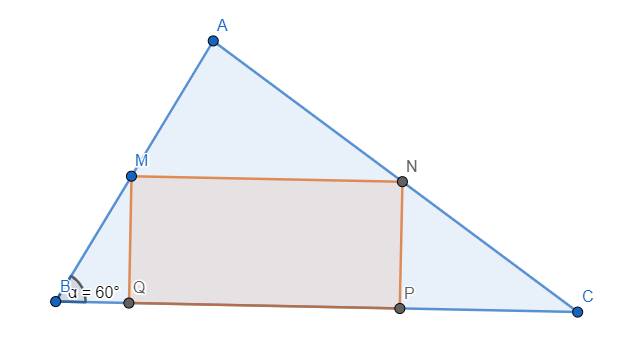
Đặt \(MB=m>0\). \(\Rightarrow MQ=NP=\dfrac{m}{\sqrt{3}}\)
Đặt \(AB=b>m\). Khi đó \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
\(\Rightarrow MN=\dfrac{AM.BC}{AB}=\dfrac{\left(b-m\right).a}{b}=\left(1-\dfrac{m}{b}\right).a\) \(=a-\dfrac{a}{b}.m\)
\(\Rightarrow S_{MNPQ}=MN.NP=\dfrac{1}{\sqrt{3}}m\left(a-\dfrac{a}{b}.m\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+bm\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+2m.\dfrac{b}{2}-\dfrac{b^2}{4}+\dfrac{b^2}{4}\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left[-\left(m-\dfrac{b}{2}\right)^2+\dfrac{b^2}{4}\right]\)
\(=-\dfrac{a}{\sqrt{3}}\left(m-\dfrac{b}{2}\right)^2+\dfrac{ab}{4\sqrt{3}}\) \(\le\dfrac{ab}{4\sqrt{3}}\), suy ra \(S_{MNPQ}\le\dfrac{ab}{4\sqrt{3}}\)
Dấu "=" xảy ra \(\Leftrightarrow m=\dfrac{b}{2}\) hay M là trung điểm của đoạn AB.
Vậy để diện tích hình chữ nhật MNPQ lớn nhất khi và chỉ khi M là trung điểm AB.