Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Ta có:
\(x^4+1=\left(x^2+ax+b\right)\left(x^2-ax+a^2-b\right)+\left(2ab-a^3\right)x+1-a^2b+b^2\)
Để \(\left(x^4+1\right)⋮\left(x^2+ax+b\right)\) thì
\(\Rightarrow\left\{{}\begin{matrix}2ab-a^3=0\\1-a^2b+b^2=0\end{matrix}\right.\) dễ thấy \(a=0\) không phải là nghiệm của hệ nên
\(\Rightarrow\left\{{}\begin{matrix}2b-a^2=0\\1-a^2b+b^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{a^2}{2}\\1-\dfrac{a^4}{2}+\dfrac{a^4}{4}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=1\\a=\pm\sqrt{2}\end{matrix}\right.\)

Vì ∆ ABC đồng dạng với ∆ AMN nên:
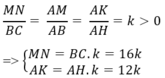
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
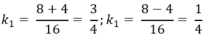
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
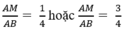

Vì ∆ ABC đồng dạng với ∆ AMN nên:
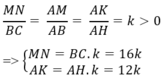
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
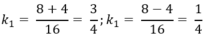
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
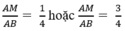


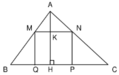
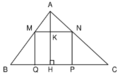
Đặt \(MB=m>0\). \(\Rightarrow MQ=NP=\dfrac{m}{\sqrt{3}}\)
Đặt \(AB=b>m\). Khi đó \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
\(\Rightarrow MN=\dfrac{AM.BC}{AB}=\dfrac{\left(b-m\right).a}{b}=\left(1-\dfrac{m}{b}\right).a\) \(=a-\dfrac{a}{b}.m\)
\(\Rightarrow S_{MNPQ}=MN.NP=\dfrac{1}{\sqrt{3}}m\left(a-\dfrac{a}{b}.m\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+bm\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+2m.\dfrac{b}{2}-\dfrac{b^2}{4}+\dfrac{b^2}{4}\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left[-\left(m-\dfrac{b}{2}\right)^2+\dfrac{b^2}{4}\right]\)
\(=-\dfrac{a}{\sqrt{3}}\left(m-\dfrac{b}{2}\right)^2+\dfrac{ab}{4\sqrt{3}}\) \(\le\dfrac{ab}{4\sqrt{3}}\), suy ra \(S_{MNPQ}\le\dfrac{ab}{4\sqrt{3}}\)
Dấu "=" xảy ra \(\Leftrightarrow m=\dfrac{b}{2}\) hay M là trung điểm của đoạn AB.
Vậy để diện tích hình chữ nhật MNPQ lớn nhất khi và chỉ khi M là trung điểm AB.