1.Cho tứ diện đều ABCD cạnh bằng a, gỏi I là trung điểm cạnh AD. Tính góc giữa hai đường thẳng AB và CI.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2023
THAM KHẢO:
Tam giác ACD đều cạnh a có AK là trung tuyến nên AK=\(\dfrac{\sqrt{3}}{2}\)a
Gọi I là trung điểm của BD
Tam giác ABD đều cạnh a có AI là trung tuyến nên AI=\(\dfrac{\sqrt{3}}{2}\)a
Tam giác BCD có IK là đường trung bình nên IK//BC, IK=\(\dfrac{1}{2}\)BC=\(\dfrac{1}{2}\)a
Ta có: cos\(\widehat{AKI}\)=\(\dfrac{\left(\dfrac{\sqrt{3}}{2}\right)^2+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{\sqrt{3}}{2}\right)^2}{2.\dfrac{\sqrt{3}}{2}.\dfrac{1}{2}}=\dfrac{\sqrt{3}}{6}\)
Nên \(\widehat{AKI}\)=\(73,2^0\)
Vì BC//IK nên góc giữa AK và BC là góc giữa AK và KI và bằng \(73,2^0\)
CM
8 tháng 5 2019
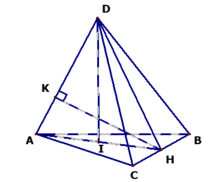
Tính khoảng cách giữa AD và BC.
● Trong ΔADH vẽ đường cao HK tức là HK ⊥ AD (1)
- Mặt khác BC ⊥ (ADH) nên BC ⊥ HK (2)
- Từ (1) và (2) ta suy ra d(AD, BC) = HK.
● Xét ΔDIA vuông tại I ta có:
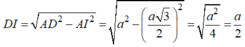
● Xét ΔDAH ta có:
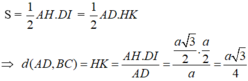
giúp em với