cho góc XOY . lấy M trong XOY . kẻ MH vuông với OX ,MK vuông góc OY . trên tia đối của tia HM lấy HN =HM. trên tia đối của tia KM lấy KB = KM . CM a)ON= OM b)ON = OB LÀM NHANH GIÚP MÌNH NHA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2014
Cứ vẽ hình ra mới hiểu nha (tui k vẽ hình ở đây được)
Xét tam giác ohn và tam giác ohm ta có :
hn=hm(gt)
góc ohm= góc ohn (=90o)
oh: cạnh chung
=>tam giác ohm= tam giác ohn
=>on=om(hai cạnh tương ứng)
(Xem đây rồi tự chứng minh câu sau nhé)
TD
10 tháng 1 2020
Xét ΔOPK và ΔOMK có:
OK chung
ˆOKM=ˆOKP=90o(MK⊥OK)OKM^=OKP^=90o(MK⊥OK)
KP=KM (gt)
⇒ΔOPK=ΔOMK(c.g.c)
⇒OP=OM (1)
Xét ΔOHM và ΔOHN có:
OH chung
ˆOHM=ˆOHN=90o(MH⊥OH)OHM^=OHN^=90o(MH⊥OH)
HM=HN (gt)
⇒ΔOHM=ΔOHN (c.g.c)
⇒ON=OM (2)
Từ (1) và (2) ⇒OP=ON
⇒đpcm
Chúc bạn học tốt. Cho mình xin 1 like để ủng hộ mình
20 tháng 3 2020
xét tam giác OMI và tam giác OAI có : OI chung
IM = IA (gt)
^OIM = ^OIA = 90
=> tam giác OMI = tam giác OAI (2cgv)
=> OM = OA (1)
xét tam giác OHM và tam giác OHB có : OH chung
HB = HM (gt)
^OHB = ^OHM = 90
=> tam giác OHM = tam giác OHB (2cgv)
=> OB = OM và (1)
=> OA = OB
VQ
20 tháng 3 2020
Hình bạn tự kẻ nha , mình ghi bải giải
Xét tam giác OAM có : OI là đường cao(Vì OI vuông góc với AM )
OI là trung tuyến(Vì I là trung điểm AM)
=> Tam giác OAM cân tại O (vì có đường cao vừa là đường trung tuyến)
=> OA = OM (1)
Xét tam giác OBM có : OH là đường cao(Vì OH vuông góc với BM)
OH là trung tuyến(Vì H là trung điểm BM)
=> Tam giác OBM cân tại O(Vì có đường cao vừa là đường trung tuyến)
=> OM = OB (2)
Từ (1) và (2) suy ra OA = OB (vì cùng bằng OM)
Học Tốt
TD
10 tháng 1 2020
Xét ΔOPK và ΔOMK có:
OK chung
\(\widehat{OKM}=\widehat{OKP}=90^o\left(MK\perp OK\right)\)
KP=KM (gt)
⇒ΔOPK=ΔOMK(c.g.c)
⇒OP=OM (1)
Xét ΔOHM và ΔOHN có:
OH chung
\(\widehat{OHM}=\widehat{OHN}=90^o\left(MH\perp OH\right)\)
HM=HN (gt)
⇒ΔOHM=ΔOHN (c.g.c)
⇒ON=OM (2)
Từ (1) và (2) ⇒OP=ON
⇒đpcm
Chúc bạn học tốt. Cho mình xin 1 like để ủng hộ mình
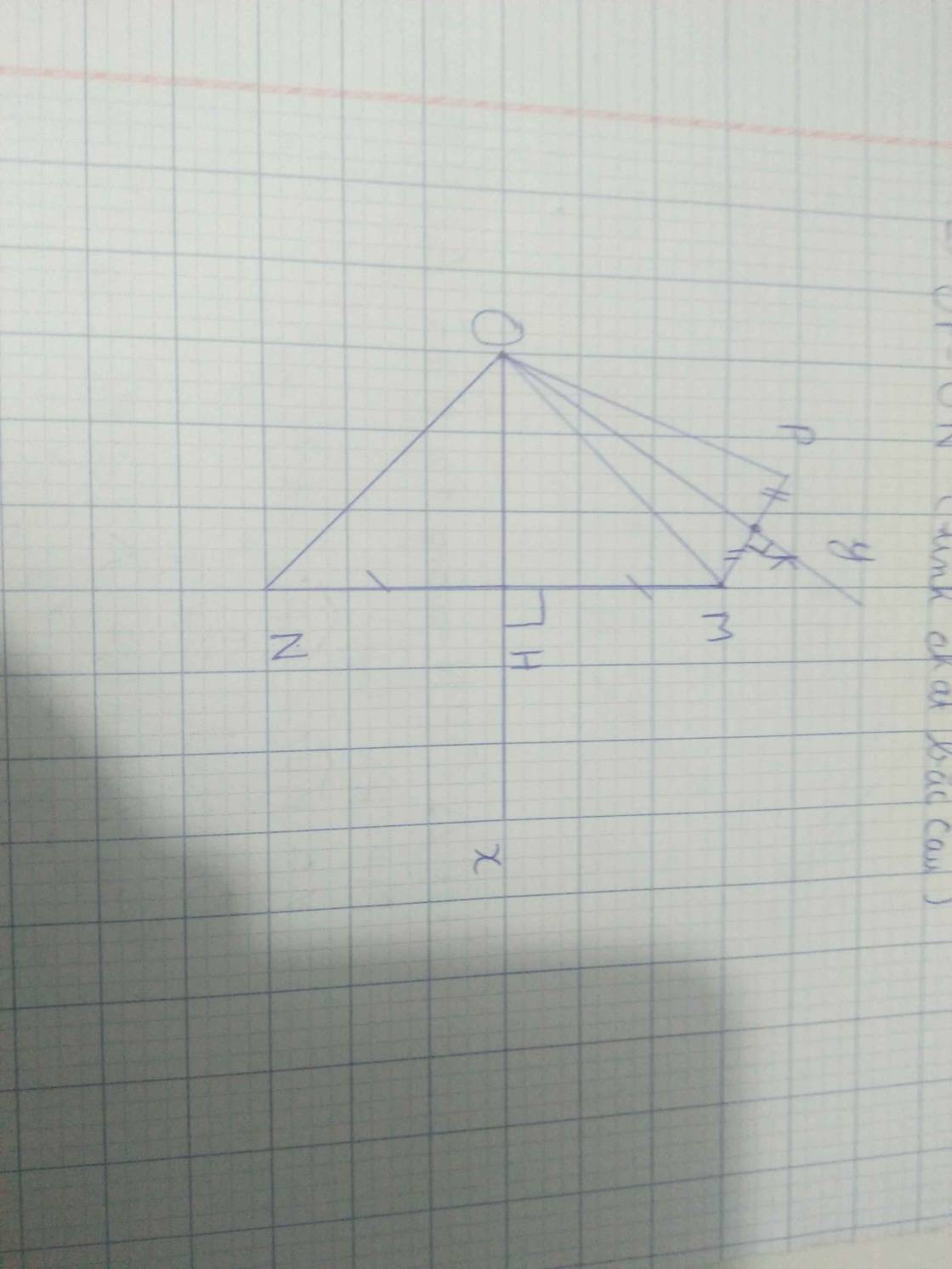
Hình: Tự vẽ....
a) Xét \(\Delta OHM\) và \(\Delta OHN\) có:
MH = NH ( theo giả thiết )
\(\widehat{MHO}=\widehat{NHO}=90^0\)
OH: cạnh chung
\(\Rightarrow\Delta OHM=\Delta OHN\left(c.g.c\right)\)
\(\Rightarrow OM=ON\) ( hai cạnh tương ứng ) (đpcm)
b) Xét \(\Delta OMK\) và \(\Delta OBK\) có:
\(MK=KB\) ( theo giả thiết )
\(\widehat{OKM}=\widehat{OKB}=90^0\)
OK: cạnh chung
\(\Rightarrow\Delta OKM=\Delta OKB\left(c.g.c\right)\)
\(\Rightarrow OM=OB\) ( hai cạnh tương ứng )
Lại có: \(ON=OM\) ( theo phần a )
\(\Rightarrow ON=OB\) ( cùng bằng OM ) (đpcm)