Một công ty muốn chạy một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo mà là 6 km từ bờ biển.Nó có giá 5000 USD mỗi km để chạy các đường ống trên bờ,13000USD mỗi km để chạy nó dưới nước.\(B^,\)trên bờ biển sao cho \(BB^,\) vuông góc với \(AB^,\) (xem như vuông góc với bờ biển ).Khoảng cách từ A đến \(B^,\)là 9km.Người ta đi đường ống từ vị trí A đến ví trí M trên đoạn \(AB^,\) và đi từ M đến B. tìm vị trí của M để chi phí là đi đường ống là thấp nhất
A.AM=0
B.AM=9
C.AM=4,5
D.AM=6,5

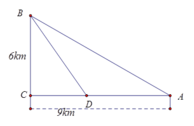
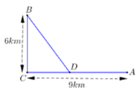




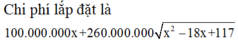
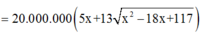

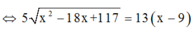
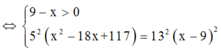


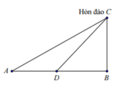
À rồi, nếu mình hiểu không nhầm thì có nghĩa là \(BB'=6(km)\)
Theo đề bài: Xét tam giác vuông tại $B'$ là $AB'B$ có điểm $M\in AB'$
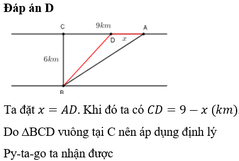
Đặt $MB'=x$. Chi phí đường ống là: \(AM.5000+13000MB=5000(9-x)+13000\sqrt{36+x^2}\)
Để chi phí min thì \(y=13000\sqrt{36+x^2}-5000x\) phải min.
Có \(y'=\frac{13000x}{\sqrt{36+x^2}}-5000=0\Leftrightarrow x=\pm 2,5\). Do đó $y$ min khi $x=2,5$, tức là $AM=9-2,5=6,5$
Do đó $D$ là đáp án đúng.
Một công ty muốn chạy một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo mà là 6 km từ bờ biển
Câu bôi đậm có nghĩa gì vậy bạn =)))