K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TA
1
Những câu hỏi liên quan
DD
2
ST
1
TF
1
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$
16 tháng 7 2023
\(tangB=\dfrac{BC}{AC}\Rightarrow AC=\dfrac{BC}{tangB}=\dfrac{6}{0,5}=12\)
11 tháng 7 2016
= x3 + 33 -x(x2 -1) -27 =0 ( tổng các lập phuong)
x =0
CX100%
MT
1
15 tháng 10 2021
Bài 5:
a) Do \(x,y\in N\)
\(\Rightarrow\left\{\left(x;y-2\right)\right\}\in\left\{\left(1;7\right),\left(7;1\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;9\right),\left(7;3\right)\right\}\)
b) Do \(x,y\in N\)
\(\Rightarrow\left(x+1;y+5\right)\in\left\{\left(1;12\right),\left(2;6\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(0;7\right),\left(1;1\right)\right\}\)
c) Do \(x,y\in N\)
\(\Rightarrow\left(x-1;2y+1\right)\in\left\{\left(18;1\right),\left(2;9\right),\left(6;3\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(19;0\right),\left(3;4\right),\left(7;1\right)\right\}\)
Trả lời:
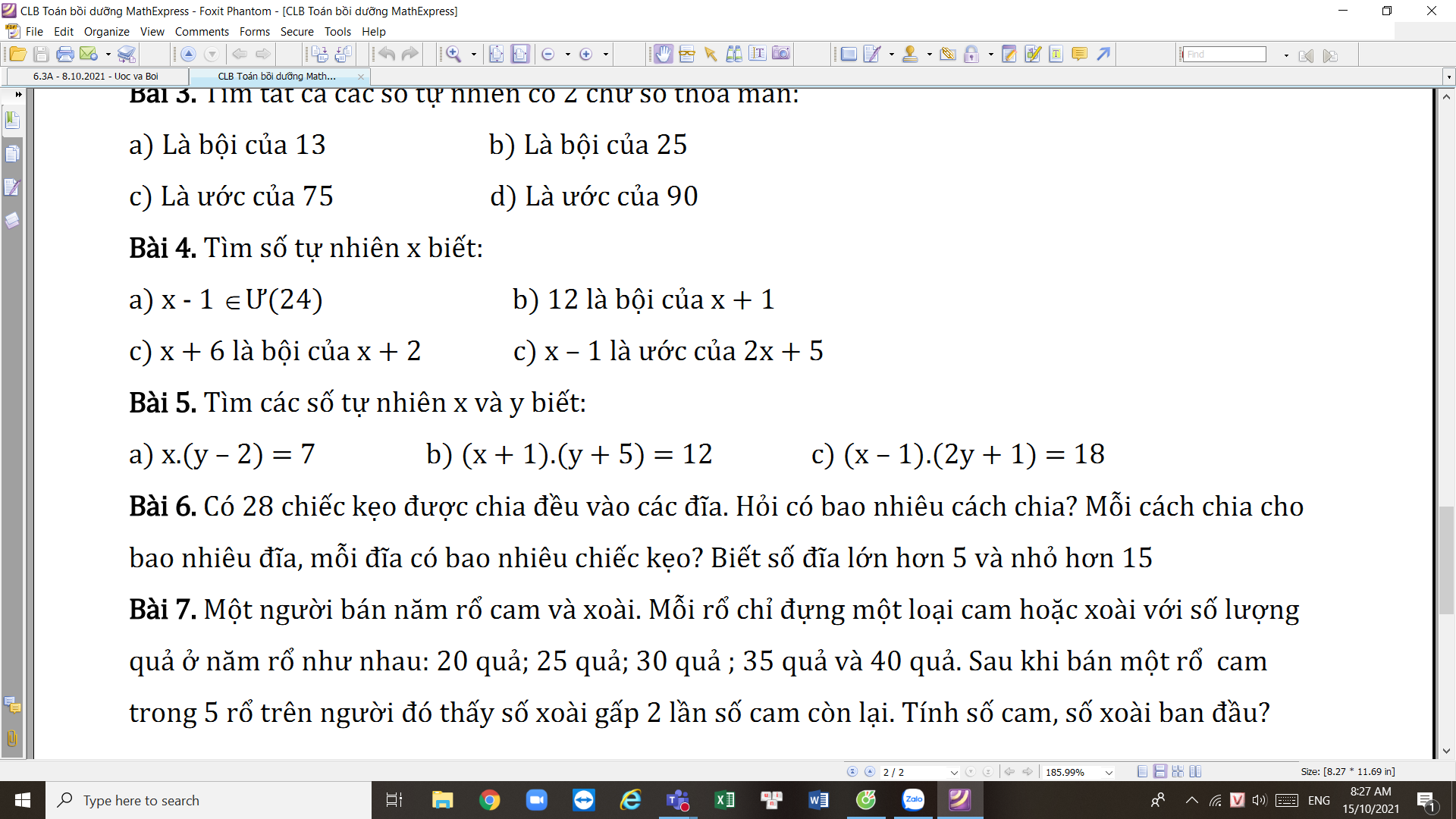
\(\sqrt{4x^2}=\sqrt{\left(2x\right)^2}=\left|2x\right|\)
+) TH1: Nếu \(x\ge0\Rightarrow\left|2x\right|=2x\)
+) TH2: Nếu \(x< 0\Rightarrow\left|2x\right|=-2x\)