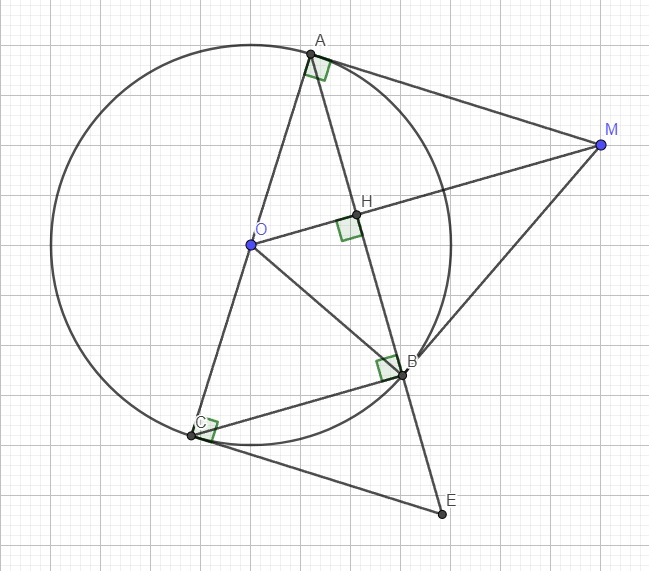
cho đt tâm O đường kính AB = 2R. Qua B kẻ tiếp tuyến d của đt (O). gọi M thuộc d (M khác B). từ B kẻ đường thẳng vuông góc OM cắt OM tại H và cắt dt (O) tại C (C khác B)
a) cm OM.OH = R2
b) cm MC là tiếp tuyến
c) từ C kẻ CK vuông góc với d tại K. Gọi I là giao điểm của CK và OM. cm M di động trên d (M khác B) thì I luôn thuộc một đường cố định