cho 8 quả cân có trọng lượng lần lượt là 1kg, 2kg, 3kg, 4kg, 5kg, 6kg, 7kg, 8kg. chọn ngẫu nhiên 3 quả cân trong số đó. tính xác suất để 3 quả cân được chọn có trọng lượng không vượt quá 9kg
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 7 2019
Đáp án C
Các trường hợp thuận lợi là 6 ; 2 ; 1 , 5 ; 3 ; 1 , 5 ; 2 ; 1 , 4 ; 3 ; 2 , 4 ; 3 ; 1 , 4 ; 2 ; 1 , 3 ; 2 ; 1
Không gian mẫu Ω = C 8 3 = 56 ⇒ p = 7 56 = 1 8
CM
7 tháng 7 2017
Đáp án C
Các trường hợp thuận lợi là (6;2;1), (5;2;1), (5;2;1), (4;3;2), (4;3;1), (4;2;1), (3;2;1).
Không gian mẫu Ω = C 8 3 = 56 ⇒ p = 7 56 = 1 8 .
CM
23 tháng 10 2017
Đáp án C
Số phần tử của không gian mẫu là số các tổ hợp chập 3 của 8 phần tử
Gọi A là biến cố “Lấy được 3 quả cân có tổng trọng lượng không vượt quá 9kg”
n(A) = 7
Xác suất xảy ra biến cố A là:
P ( A ) = 7 56 = 1 8 a
AH
Akai Haruma
Giáo viên
1 tháng 12 2019
Lời giải:
Chọn ngẫu nhiên 3 quả cân trong số 8 quả cân, có $C^3_8=56$ cách chọn
Chọn 3 quả cân mà trọng lượng không vượt quá 9 kg có các TH sau:
$(1,2,3); (1,2,4); (1,2,5); (1,2,6); (1,3,4); (1,3,5); (2,3,4)$ (có 7 cách chọn)
Do đó xác suất để chọn được 3 quả cân có trọng lượng không vượt quá 9kg là: $\frac{7}{56}=\frac{1}{8}$
CM
29 tháng 10 2017
Đáp án D
Chọn ngẫu nhiên 3 quả cân từ 8 quả cân có 
cách.
Suy ra 
Gọi A là biến cố: “chọn được 3 quả cân có tổng khối lượng không quá 9kg”
Khi đó A={(1;2;3), (1;2;4), (1;2;6), (1;3;4), (1;3;5), (2;3;4)}
Suy ra n(A)=7
Vậy xác suất cần tìm là
CM
12 tháng 4 2017
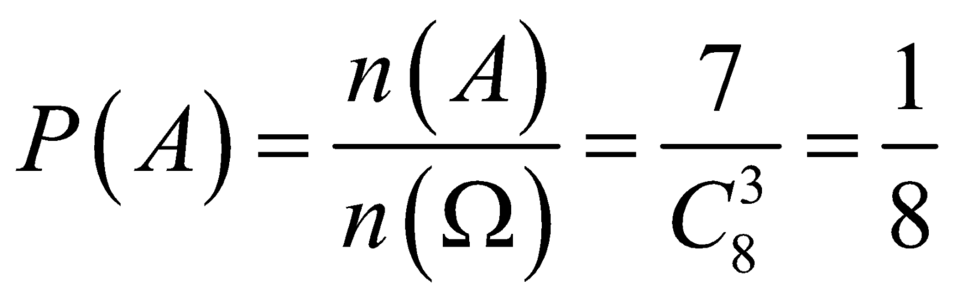
Chọn ngẫu nhiên 3 quả cân từ 8 quả cân
Gọi A là biến cố: “chọn được 3 quả cân có tổng khối lượng không quá 9kg”
Khi đó A = {(1;2;3); (1;2;4); ( 1;2;5); (1;2;6); (1;3;4); (1;3;5); (2;3;4)}
Suy ra n(A) = 7
Vậy xác suất cần tìm là P A = n A n Ω = 7 C 8 3 = 1 8
Đáp án D
4 tháng 8
Để chia 3,6 kg đường thành 3 gói cân nặng 2 kg, 1 kg và 600 g chỉ với 2 lần cân và 2 quả cân 200 g, bạn có thể thực hiện theo các bước như sau: ### **Bước 1: Cân gói 2 kg** 1. **Đặt 2 quả cân 200 g (tổng cộng 400 g) lên một bên của cân.** 2. **Đặt đường vào bên còn lại của cân cho đến khi cân bằng.** - Khi đạt được sự cân bằng, bạn sẽ có **2 kg đường** ở bên còn lại, vì 2 kg + 0.4 kg (từ quả cân) sẽ cân bằng. ### **Bước 2: Cân gói 600 g** 1. **Lấy 2 kg đường ra khỏi cân.** 2. **Đặt tiếp 200 g đường ở bên của cân (tổng cộng 400 g từ 2 quả cân).** 3. **Đặt đường vào bên còn lại của cân cho đến khi cân bằng.** - Khi đạt được sự cân bằng ở lần này, bạn sẽ có **600 g đường** ở bên còn lại (tức là 600 g + 0.4 kg = 1 kg). ### **Kết quả cuối cùng:** - Sau 2 lần cân, bạn đã có: - **1 gói 2 kg** - **1 gói 600 g** - **Còn lại 600 g đường, bạn sẽ có gói còn lại là 1 kg (3.6 kg - 2 kg - 600 g = 1 kg).** Như vậy, bạn đã chia được 3,6 kg đường thành 3 gói: **2 kg, 1 kg, và 600 g.**
Gọi A là biến cố chọn được 3 quả cân có tổng trọng lượng không vượt quá 9 kg.
Suy ra A có các trường hợp sau:
A = { (1, 2, 3); (1, 2, 4); (1, 2, 5); (1, 2, 6); (1, 3, 4); (1, 3, 5); (2, 3, 4)}
⇒P=7C38=18⇒P=7C83=18
Vậy xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg là: 18