Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn ngẫu nhiên 3 quả cân từ 8 quả cân
Gọi A là biến cố: “chọn được 3 quả cân có tổng khối lượng không quá 9kg”
Khi đó A = {(1;2;3); (1;2;4); ( 1;2;5); (1;2;6); (1;3;4); (1;3;5); (2;3;4)}
Suy ra n(A) = 7
Vậy xác suất cần tìm là P A = n A n Ω = 7 C 8 3 = 1 8
Đáp án D

Ta có :
\(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}=\frac{2\sqrt{x}-10}{\sqrt{x}-5}+\frac{13}{\sqrt{x}-5}=2+\frac{13}{\sqrt{x}-5}\)là số nguyên dương
<=> 13 chia hết cho \(\sqrt{x}-5\)
<=> \(\sqrt{x}-5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
<=> \(\sqrt{x}\in\left\{-12;4;6;18\right\}\)
<=> \(x\in\left\{16;36;324\right\}\) (vì \(\sqrt{x}\ge0\))
Do x nguyên và x có GTLN nên x = 324

∆ M N P có trọng tâm G ( 3;6;-3 ). Đường thẳng d qua G và vuông góc với (Q) có phương trình
x = 3 + t y = 6 + 2 t z = - 3 - t
K = d ∩ Q tọa độ điểm K ứng với tham số t là nghiệm của phương trình:
3 + t + 2 6 + 2 t - - 3 - t - 6 = 0 ⇔ t = - 2 ⇒ K 1 ; 2 ; - 1
Đáp án D

Đáp án A
Ta có V G ; − 1 2 A = A ' ⇒ G A ' → = − 1 2 G A → ⇒ A ' là trung điểm của B ' C '
Tương tự, ta thấy B ' C ' lần lượt là trung điểm của A ' C ' , A ' B ' ⇒ S Δ A ' B ' C ' S Δ A B C = 1 4
Vậy tỉ số V S . A ' B ' C ' V S . A B C = d S ; A B C . S Δ A ' B ' C ' d S ; A B C . S Δ A B C = 1 4

Đáp án A
Do Δ A ' B ' C ' là ảnh của Δ A B C qua phép V G ; K = − 1 2
Do đó: S A ' B ' C ' S A B C = k 2 = 1 4 ⇒ V A ' B ' C ' V A B C = d S ; A B C . S A ' B ' C ' d S ; A B C . S A B C = 1 4

Thay K(0) = 4 vào đa thức K(x) ta có : a.0^2 + b.0 + c => c = 4 (1)
Thay K(1) = 3 và (1) vào đa thức K(x) ta có : a.1^2 + b.1 + 4 = a + b + 4 = 3 => a+b=-1 => a= -1 - b (2)
Thay K(-1) = 7 , (1) vào đa thức K(x) ta có : a.(-1)^2 + b.(-1) + 4 = a-b+4=7 => a-b=3 (3)
Thay (2) vào (3) ta có : -1 - b - b = -1 - 2b = 3 => 2b= -4 => b = -2
Thay b = -2 vào (3) ta có : a - (-2) = 3 => a = 1.
Vậy a + b + c = 1 + (-2) + 4 = 3

\(\dfrac{1}{k^2}<\dfrac{1}{k(k-1)}=\dfrac{1}{k-1}-\dfrac{1}{k}\)
Ap dung:
\(\dfrac{1}{1^2}+\dfrac{1}{2^2}+\ldots+\dfrac{1}{n^2}<1+\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\ldots+\left(\dfrac{1}{n-1}-\dfrac{1}{n}\right)=2-\dfrac{1}{n}<2\)
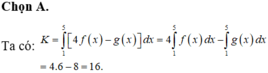
Đáp án C
Các trường hợp thuận lợi là 6 ; 2 ; 1 , 5 ; 3 ; 1 , 5 ; 2 ; 1 , 4 ; 3 ; 2 , 4 ; 3 ; 1 , 4 ; 2 ; 1 , 3 ; 2 ; 1
Không gian mẫu Ω = C 8 3 = 56 ⇒ p = 7 56 = 1 8