Thầy cô giải bài này giúp e vs ạ, thanks
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
Đỗ Thanh Hải
CTVVIP
1 tháng 8 2021
37 distinguish
38 illiteracy
39 energetic
40 disconnected
41 anxiety
42 mysteriously
43 significant
44 frightening
45 repeatedly
46 cancellation
47 disastifying
48 products
49 disagree
50 typicallu
51 socialize
52 vegetarian
53 entrance
54 modernized
55 income
NT
1
DT
Đỗ Thanh Hải
CTVVIP
1 tháng 8 2021
1 inconvenience
2 voluntarily
3 industrial
4 break-taking
5 intentively
6 breakdown
7 preferable
8 economical
9 acceleration
10 misunderstanding
11 inhabitant
12 kidnapper
13 foggy
14 shouthern
15 decision
16 entertainment
17 information
18 pronounciation
NA
7 tháng 7 2016
a) \(10^5+35=100000+35=100035\)
Vì 100035 có chữ số tận cùng là 5 nên nó chia hết cho 5
Vì 100035 có tổng tất cả các chữ số bằng 9 nên nó chia hết cho 9
b) \(10^5+98=100000+98=100098\)
Để 100098 chia hết cho 18 thì 100098 phải chia hết cho 2 và 9 mà 100098 có chữ số tận cùng là số chẵn (8) và tổng của tất cả các chữ số bằng 18 nên 100098 chia hết cho 2 và 9. Vậy 100098 chia hết cho 18.
7 tháng 7 2016
a) Ta có : \(10^5+35=100000+35=100035\)
+) Vì 100035 tận cùng là 5 => 100035 chia hết cho 5
=> \(10^5+35\) chia hết cho 5
+) Ta có : \(100035=1+0+0+0+3+5=9\)
Để \(10^5+35\) chia hết cho 9 <=> \(10^{35}+35\) có tổng các chữ số của nó chia hết cho 9
Mà 9 chia hết cho 9 => 100035 chia hết cho 9
=> \(10^5+35\) chia hết cho 9
Vậy \(10^5+35\) vừ chia hết cho 5 vừa chia hết cho 9 ( đpcm )
b) Ta có : \(10^5+98=100000+98=100098\)
Vì \(18=2.9\) => Để \(10^5+98\) chia hết cho 18 <=> \(10^5+98\) chia hết cho cả 2 và 9
+) Vì 100098 tận cùng là số chẵn ( 8 )
=> 100098 chia hết cho 2 => \(10^5+98\) chia hết cho 2
+) Ta có : \(100098=1+0+0+0+9+8=18\)
Mà 18 chia hết cho 9
=> 100098 chia hết cho 9
=> \(10^5+98\) chia hết cho 9
Vì \(10^5+98\) vừa chia hết cho 9 vừa chia hết cho 2
=> \(10^5+98\) chia hết cho 18 ( đpcm )
TT
1
25 tháng 3 2023
1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1
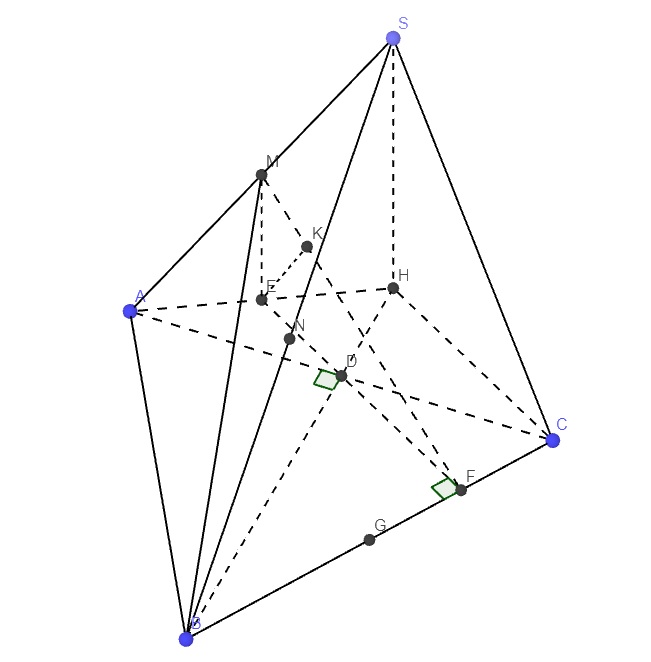
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)
DT
Đỗ Thanh Hải
CTVVIP
1 tháng 8 2021
76 successful
77 richness
78 musician
79 pollution
80 saving
81 unpleasant
82 misinformed
83 favorable
84 encouragement
85 qualified
86 traditionally
87 dressed
88 invention
89 musician
90 ability
91 nervousness
92 confidence
93 independently
94 endlessly
95 breakthrough
96 lessen
97 penniless
98 pursuit
99 Contended
100 situation
101 expectation
102 variety
103 logical
