Tính : A = 13 + 23 + 33 + .................. + n3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có 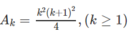
Ta có:
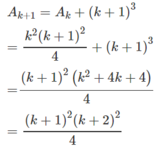

A) =(5+(-15))+(9+(-19))+(-11)+(13+17)+(21+(-23))
=(-10)+(-10)+(-11)+20+(-2)
=((-10)+(-10))+(-11)+(-2)+20
=(-20)+(-11)+20+(-2)
=((-20)+20)+((-11)+(-2))
=0+(-13)=-13
B) doi ti !!!!! Tich cho mik nha

S = 13+10+23+20+33+30+...+103+100
S = 13+23+33+...+103+10.100
S = 3025+1000
S = 4025


A=7*(1/3*13+1/13*23+1/23*33+1/33*43+1/43*53+1/53*63)
A=7/10(1/3-1/13+1/13-1/23+1/23-1/33+1/33-1/43+1/43-1/53+1/53-1/63)
A=7/10*(1/3-1/63)
A=7/10*20/63
A=2/9

\(\frac{\frac{6}{13}-\frac{6}{23}+\frac{6}{33}-\frac{6}{43}}{\frac{5}{13}-\frac{5}{23}+\frac{5}{33}-\frac{5}{43}}\)
= \(\frac{6.\left(\frac{1}{13}-\frac{1}{23}+\frac{1}{33}-\frac{1}{43}\right)}{5.\left(\frac{1}{13}-\frac{1}{23}+\frac{1}{33}-\frac{1}{43}\right)}\)
= \(\frac{6}{5}\)
k cho mình nhé

a, 2 17 + 17 2 9 15 - 3 15 2 4 - 4 2
= 2 17 + 17 2 9 15 - 3 15 16 - 16
= 2 17 + 17 2 9 15 - 3 15 . 0
= 0
b, 1 2 + 2 3 + 3 4 + 4 5 . ( 1 3 + 2 3 + 3 3 + 4 3 ) ( 3 8 - 81 2 )
= 1 2 + 2 3 + 3 4 + 4 5 . ( 1 3 + 2 3 + 3 3 + 4 3 ) ( 3 4 . 2 - 81 2 )
= 1 2 + 2 3 + 3 4 + 4 5 . ( 1 3 + 2 3 + 3 3 + 4 3 ) ( 81 2 - 81 2 )
= 1 2 + 2 3 + 3 4 + 4 5 . ( 1 3 + 2 3 + 3 3 + 4 3 ) . 0
= 0
c, 7 24 + 7 23 : 7 22
= 7 24 : 7 22 + 7 23 : 7 22
= 7 24 - 22 + 7 23 - 22
= 7 2 + 7 1
= 49 + 7 = 56

13 + 23 + 33 + 33 + 53 = a.a
155 = a.a
\(\left[{}\begin{matrix}-\sqrt{155}\\\sqrt{155}\end{matrix}\right.\)
a \(\in\) {\(-\sqrt{155}\); \(\sqrt{155}\)}
13+23+33+..n3=(1+2+3+...+n)213+23+33+..n3=(1+2+3+...+n)2
Với n=1;n=2n=1;n=2 thì đẳng thức hiển nhiên đúng
Giả sử đẳng thức đúng với n=kn=k
Tức 13+23+33+...k3=(1+2+3+4..+k)213+23+33+...k3=(1+2+3+4..+k)2
Ta sẽ chứng minh nó đúng với n=k+1n=k+1
Viết lại đẳng thức cần chứng minh 13+23+33+...k3+(k+1)3=(1+2+3+4..+k+k+1)213+23+33+...k3+(k+1)3=(1+2+3+4..+k+k+1)2 (*)
Mặt khác ta có công thức tính tổng sau 1+2+3+4+...+n=n(n+1)21+2+3+4+...+n=n(n+1)2
⇒(1+2+3+4+...+n)2=(n2+n)24⇒(1+2+3+4+...+n)2=(n2+n)24
\(A=1^3+2^3+3^3+...+n^3\)
\(\Rightarrow A=\left(1+2+3+...+n\right)^2\)
\(\Rightarrow A=\left(n\times\left(n+1\right)\div2\right)^2\)