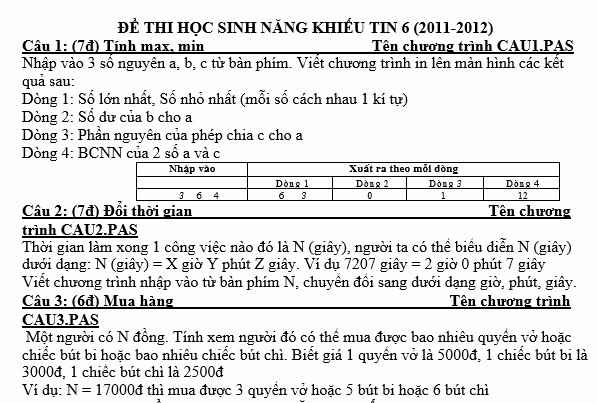
Làm được bài nào thì làm...
Đọc tiếp
Làm được bài nào thì làm nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
4
13 tháng 11 2021
#include <bits/stdc++.h>
using namespace std;
double a,b,c,p,s;
int main()
{
cin>>a>>b>>c;
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
cout<<fixed<<setprecision(2)<<p;
return 0;
}
13 tháng 11 2021
1:
uses crt;
var a,b,c,max,min:longint;
begin
clrscr;
readln(a,b,c);
max=a;
if max<b then max:=b;
if max<c then max:=c;
min:=a;
if min>c then min:=c;
if min>b then min:=b;
writeln(max,' ',min);
readln;
end.
HN
20 tháng 11 2021
Số điểm 25 câu đúng được:
25.3 = 75 (điểm)
Bạn An đã bị trừ:
75 - 69 = 6 (điểm)
Theo đề bài, nếu làm sai thì mỗi câu bị trừ 2 điểm, An bị trừ tổng cộng 6 điểm, nghĩa là An đã sai:
6 : 2 = 3 (câu)
Đáp số: 3 câu.
DT
1
E
7
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
V.
\(95^8< 100^8=10^{16}\)
Mà \(10^{16}\) có 17 chữ số nên \(95^8\) có ít hơn 17 chữ số (1)
Lại có: \(95^8>90^8=10^8.9^8=10^8.81^4>10^8.80^4=10^{12}.2^{12}>10^{12}.2^{10}>10^{12}.10^3=10^{15}\)
\(\Rightarrow95^8\) có nhiều hơn 15 chữ số (2)
Từ (1) và (2) \(\Rightarrow95^8\) có 16 chữ số trong cách viết ở hệ thập phân
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
III.
1. Xét hiệu:
\(A-B=\dfrac{2019^{2020}+1}{2019^{2019}+1}-\dfrac{2019^{2019}+1}{2019^{2018}+1}=\dfrac{\left(2019^{2020}+1\right)\left(2019^{2018}+1\right)-\left(2019^{2019}+1\right)^2}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2019^{4028}+1+2019^{2020}+2019^{2018}-2019^{4028}-2.2^{2019}-1}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2019^{2020}-2019^{2019}+2019^{2018}-2019^{2019}}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2019^{2019}\left(2019-1\right)-2019^{2018}\left(2019-1\right)}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2018.2019^{2019}-2018.2019^{2018}}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}=\dfrac{2018.2019^{2018}\left(2019-1\right)}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2018^2.2019^{2018}}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}>0\)
\(\Rightarrow A>B\)
TH
0
20 tháng 4 2021
Bài 1:
b) Ta có: \(\dfrac{x-12}{77}+\dfrac{x-11}{78}=\dfrac{x-74}{15}+\dfrac{x-73}{16}\)
\(\Leftrightarrow\dfrac{x-12}{77}-1+\dfrac{x-11}{78}-1=\dfrac{x-74}{15}-1+\dfrac{x-73}{16}-1\)
\(\Leftrightarrow\dfrac{x-89}{77}+\dfrac{x-89}{78}-\dfrac{x-89}{15}-\dfrac{x-89}{16}=0\)
\(\Leftrightarrow\left(x-89\right)\left(\dfrac{1}{77}+\dfrac{1}{78}-\dfrac{1}{15}-\dfrac{1}{16}\right)=0\)
mà \(\dfrac{1}{77}+\dfrac{1}{78}-\dfrac{1}{15}-\dfrac{1}{16}\ne0\)
nên x-89=0
hay x=89
Vậy: S={89}
20 tháng 4 2021
Bài 1:
a)ĐKXĐ: \(x\notin\left\{3;-1\right\}\)
Ta có: \(\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2x+2}=\dfrac{2x}{\left(x-3\right)\left(x+1\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x-3\right)\left(x+1\right)}\)
Suy ra: \(x^2+x+x^2-3x-4x=0\)
\(\Leftrightarrow x^2-6x=0\)
\(\Leftrightarrow x\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhân\right)\\x=6\left(nhận\right)\end{matrix}\right.\)
Vậy: S={0;6}