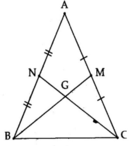
Tam giác ABC có goác A=60đ, phân giác BM và CN cắt nhau tại I chứng minh BN+CM=BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 12 2017
A C B N M I N' M'
Đề này ko đúng, bên trên là hình vẽ minh họa.
BN + CM = BN' + CM' khác BC.
CH
Cô Hoàng Huyền
Admin
VIP
17 tháng 1 2018
Câu hỏi của Công chúa thủy tề - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.
MH
19 tháng 1 2020
Chứng minh bất đẳng thức
\(\frac{x}{2x+y+z}+\frac{y}{2y+z+x}+\frac{z}{2z+x+y}\le\frac{3}{4}\)
Con này mất dạy v:, chuyện đó tính sau
肖战 - Trang của 肖战 - Học toán với OnlineMath
Nó copy dữ dội trên này lắm
Câu hỏi của 凯原 - Ngữ Văn lớp 7 - Học toán với OnlineMath
Câu hỏi của Phương' ss ngốc - Ngữ Văn lớp 7 - Học toán với OnlineMath
Câu hỏi của Khanh Linh Ha - Toán lớp 7 - Học toán với OnlineMath
Câu hỏi của kudoshinichi - Tiếng Việt lớp 5 - Học toán với OnlineMath
Còn nhiù nhưng ko có t/g để cop
22 tháng 12 2021
a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...
14 tháng 9 2023
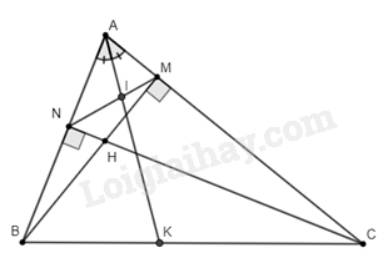
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).
7 tháng 1 2023
a: Xét ΔABD và ΔAMD có
AB=AM
góc BAD=góc MAD
AD chung
Do đó; ΔABD=ΔAMD
b: Xét ΔDBN và ΔDMC có
góc DBN=góc DMC
DB=DM
góc BDN=góc MDC
Do đó; ΔDBN=ΔDMC
=>BN=MC
c: Xét ΔANC có AB/BN=AM/MC
nên BM//CN
5 tháng 3 2021
a.Ta có:
ˆBID=12ˆBIC=12(180o−ˆBCI−ˆIBC)=12(180o−12ˆBCA−12ˆABC)=12(180o−12(ˆBCA+ˆABC)=12(180o−12(180o−ˆBAC)=60oBID^=12BIC^=12(180o−BCI^−IBC^)=12(180o−12BCA^−12ABC^)=12(180o−12(BCA^+ABC^)=12(180o−12(180o−BAC^)=60o
Lại có :
ˆNIB=ˆIBC+ˆICB
=1/2ˆABC+1/2ˆACB
=1/2(ˆABC+ˆACB)
=1/2(180o−ˆBAC)=60o
NIB^=IBC^+ICB^
=1/2ABC^+1/2ACB^
=1/2(ABC^+ACB^
=1/2(180o−BAC^)=60o
=>ˆNIB=ˆBID
=>ΔNIB=ΔDIB(g.c.g)
=>BN=BD(cmt)
b.Chứng minh tương tự câu a
→CD=CM
→BN+CM=BD+CD=BC→đpcm