cho con lắc lò xo có độ cứng k=50n/m dao động điều hòa theo phương thẳng đứng với tần số gcs là 10 rad/s.Chọn gốc tọa độ O ở vị trí cân bằng,chiều dương hướng lên và khi v=0 thì lò xo không biến dạng .Lực đàn hồi tác dụng vào vật khi vtj đang đi lên với vận tốc v=+80 cm/s =?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Độ biến dạng của lò xo tại vị trí cân bằng
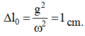
Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều dương. Thời điểm lò xo không biến dạng lần đầu tiên ứng với li độ x = - ∆ l = - 1 cm
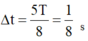
Đáp án D

ü Đáp án D

+ Độ biến dạng của lò xo tại vị trí cân bằng
Δ l 0 = g 2 ω 2 = 1 c m
Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều dương. Thời điểm lò xo không biến dạng lần đầu tiên ứng với li độ x = - Δ l 0 = - 1 c m
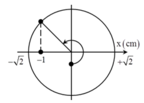
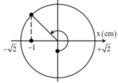
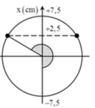
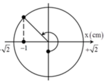
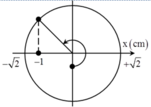
+ Biểu diễn các vị trí trên hình vẽ, ta được:
Δ t = 5 T 8 = 1 8 s

Đáp án D
Độ biến dạng của lò xo tai vị trí cân bằng ![]() cm
cm
Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều dương. Thời điểm lò xo không biến dạng lần đầu tiên ứng với li độ ![]() cm.
cm.
Biểu diễn các vị trí trên hình vẽ, ta được: 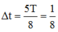 s
s

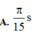
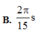
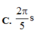
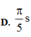


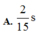
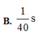
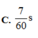
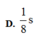


Độ giãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0\)
\(\Rightarrow \omega=\sqrt{\dfrac{g}{\Delta\ell_0}}\)
\(\Rightarrow \Delta\ell_0=\dfrac{g}{\omega^2}=\dfrac{10}{10^2}=0,1m=10cm\)
v = 0 thì lò xo không biến dạng, lúc đó \(x=\Delta\ell_0=10cm\)
Suy ra vị trí đó là ở biên, ta có: \(A=10cm\)
Khi \(v=80cm/s\) ta có: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow x^2=10^2-\dfrac{80^2}{10^2}\)
\(\Rightarrow x = \pm6cm\)
Lực đàn hồi: \(F_{dh}=k.\Delta\ell=k.|\Delta\ell_0+x|=50.|0,1\pm 0,06|\)
Suy ra \(F_{dh}=8N\)
Hoặc \(F_{dh}=2N\)