Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
? Lời giải:

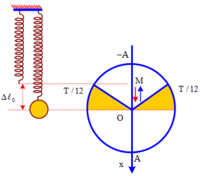
+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng

+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
![]()

Chọn đáp án A
? Lời giải:
+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
f = 1 2 π g Δ l ⇒ Δ l = 1 c m A = Δ l 2 + v 2 ω 2 = 2 c m ⇒ Δ l = A 2
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
Δ t = 2. T 12 = T 6 = 1 30 s

Chọn đáp án A
Δ l = m g k = T 2 4 π 2 g = 0 , 04 m = 4 c m T h ờ i g i a n t ừ x = 0 → x = + A → x = 0 → x = − A 2 T 4 + T 4 + T 12 = 7 T 12 = 7 30 s là:
Tốc độ trung bình:
v = s t = A + A + 0 , 5 A t = 85 , 7 c m / s

Đáp án A
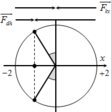
+ Độ biến dạng của lò xo tại vị trí cân bằng 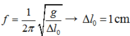
→ Biên độ dao động của con lắc 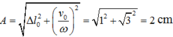
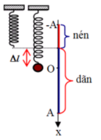
+ Trong một chu kì dao động, lực kéo về luôn hướng về vị trí cân bằng, lực đàn hồi lại luôn hướng về vị trí lò xo không biến dạng (có li độ x = - ∆ l 0 như hình vẽ)
→ Thời gian hai lực này ngược chiều nhau là 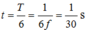

Chọn D

+ T = 1s => ω = 2π rad/s.
+ Độ biến dạng của lò xo ở vị trí cân bằng:
![]()
+ Biên độ dao động:
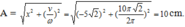
+ Thời điểm t = 0 tương ứng với một gốc lùi Δφ = ωt = 2π.2,5 = 5π trên đường tròn.
+ Lực đàn hồi khi đó có độ lớn:
Fđh = k(Δlo + x) = k(25 + 5√2). 10-2 N.
Kết hợp với Fđhmin = k.(Δlo - A) = k. 15.10-2 = 6N.
+ Từ hai biểu thức trên ta thu được Fđh = 12,82N.

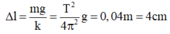
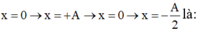
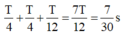
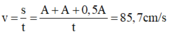

Độ giãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0\)
\(\Rightarrow \omega=\sqrt{\dfrac{g}{\Delta\ell_0}}\)
\(\Rightarrow \Delta\ell_0=\dfrac{g}{\omega^2}=\dfrac{10}{10^2}=0,1m=10cm\)
v = 0 thì lò xo không biến dạng, lúc đó \(x=\Delta\ell_0=10cm\)
Suy ra vị trí đó là ở biên, ta có: \(A=10cm\)
Khi \(v=80cm/s\) ta có: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow x^2=10^2-\dfrac{80^2}{10^2}\)
\(\Rightarrow x = \pm6cm\)
Lực đàn hồi: \(F_{dh}=k.\Delta\ell=k.|\Delta\ell_0+x|=50.|0,1\pm 0,06|\)
Suy ra \(F_{dh}=8N\)
Hoặc \(F_{dh}=2N\)