Cho y = x3- 3mx2 + (m-1)x + 1 (C), tìm m để y = -x+1 cắt (C) tại 3 điểm phân biệt.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hoành độ giao điểm của (C) và Ox là nghiệm phương trình
x - 1 x 2 - 3 m - 1 x + 1 = 0 ⇔ x = 1 g x = x 2 - 3 m - 1 x + 1 = 0 1
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt thì (1) có 2 nghiệm phân biệt khác 1.
Khi đó ∆ > 0 g 1 ≠ 0
⇔ m > 1 m < - 1 3 m ≠ 1 ⇔ m > 1 m < - 1 3
Giả sử x 3 = 1
Theo đề thì phương trình (1) có hai nghiệm x 1 ; x 2
x 1 2 + x 2 2 > 14 ⇔ x 1 + x 2 2 - 2 x 1 x 2 > 14 ⇔ m > 5 3 m < - 1
(thỏa mãn)
Vậy m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
Đáp án C

Đáp án C
Số giao điểm của đường thẳng y = ( m - 1 ) x và đồ thị hàm số y = x 3 - 3 x 2 + m + 1 là số nghiệm của PT x 3 - 3 x 2 + m + 1 = ( m - 1 ) x ⇔ x 3 - 3 x 2 + x + 1 - m x + m = 0 ⇔ ( x - 1 ) ( x 2 - 2 x - m - 1 ) = 0 để tồn tại ba giao điểm phân biệt thì 1 - 2 - m - 1 ≢ 0 ∆ ' = 1 + m + 1 > 0 ⇔ m ≢ - 2 m > - 2 khi đó tọa độ ba giao điểm là B ( 1 ; m - 1 ) , A ( x 1 ; y 1 ) , C ( x 2 ; y 2 ) hơn nữa x 1 + x 2 2 = 1 y 1 + y 2 2 = ( m - 1 ) x 1 + ( m - 1 ) x 2 2 = ( m - 1 ) ( x 1 + x 2 ) 2 = m - 1
⇒ B là trung điểm AC hay ta có AB=BC

Đáp án B
y = x 3 − 3 x + 1 y ' = 3 x 2 − 3 y ' = 0 ⇒ x = ± 1
⇒ − 1 < m < 3

Chọn B.
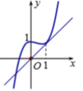
Để (C) cắt trục hoành tại 3 điểm phân biệt thì phương trình
x 3 - x 2 - m x + 1 = 0 có ba nghiệm phân biệt, hay phương trình
x 3 - x 2 + 1 = m x có ba nghiệm phân biệt.
Điều này tương đương với đường thẳng y = mx cắt đồ thị hàm số y = x 3 - x 2 + 1 tại 3 điểm phân biệt.
Đường thẳng y = mx đi qua gốc tọa độ.
Đường thẳng y = x là tiếp tuyến với đồ thị hàm số y = x 3 - x 2 + 1 (như hình minh họa trên).
Do đó với m > 1 thì đường thẳng y = mx cắt đồ thị hàm số y = x 3 - x 2 + 1 tại 3 điểm phân biệt.

Chọn B.
Cách 1:
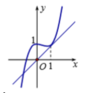
Để (C) cắt trục hoành tại 3 điểm phân biệt thì phương trình ![]() có ba nghiệm phân biệt, hay phương trình
có ba nghiệm phân biệt, hay phương trình ![]() có ba nghiệm phân biệt.
có ba nghiệm phân biệt.
Điều này tương đương với đường thẳng y = mx cắt đồ thị hàm số ![]() tại 3 điểm phân biệt.
tại 3 điểm phân biệt.
Đường thẳng y = mx đi qua gốc tọa độ.
Đường thẳng y = x là tiếp tuyến với đồ thị hàm số ![]() (như hình minh họa trên).
(như hình minh họa trên).
Do đó với m > 1 thì đường thẳng y = mx cắt đồ thị hàm số ![]() tại 3 điểm phân biệt.
tại 3 điểm phân biệt.
Cách 2:
Để (C) cắt trục hoành tại 3 điểm phân biệt thì phương trình ![]() có ba nghiệm phân biệt.
có ba nghiệm phân biệt.
Dễ thấy x = 0 không thể là nghiệm nên ![]()
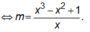
Xét hàm số 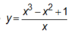 trên tập
trên tập ![]()
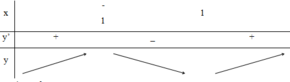
Ta có bảng biến thiên sau:
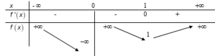
Để phương trình 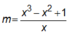 có 3 nghiệm phân biệt khi và chỉ khi m > 1.
có 3 nghiệm phân biệt khi và chỉ khi m > 1.

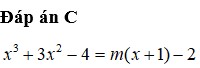
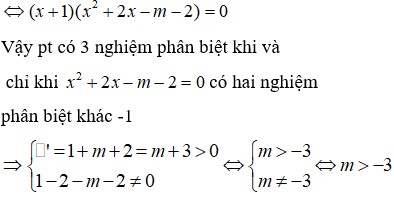
pthdgd: x3-3mx2+(m+1)x+1=-x+1<=>x3-3mx2+(m+1)x+x=0<=>x(x2-3mx+m-1+1)<=>x=0 va x2-3mx+m=0(*). de y cat (c) tai 3 diem pbiet thi (*) fai co 2 nghiem pbiet # 0<=>Δ>0. giai Δ va ket hop vs dieu kiem tim ra m