Giải thích giúp mình từng câu với ạ! Mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


12.
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)
\(\Rightarrow M=\sqrt{2}\)
13.
Pt có nghiệm khi:
\(5^2+m^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow2m\le24\)
\(\Rightarrow m\le12\)
14.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=k2\pi\)
15.
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
Đáp án A
16.
\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)
Có \(1008+1008=2016\) nghiệm


1.
\(sin^2x-4sinx.cosx+3cos^2x=0\)
\(\Rightarrow\dfrac{sin^2x}{cos^2x}-\dfrac{4sinx}{cosx}+\dfrac{3cos^2x}{cos^2x}=0\)
\(\Rightarrow tan^2x-4tanx+3=0\)
2.
\(\Leftrightarrow\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
3.
\(\Leftrightarrow2^2+m^2\ge1\)
\(\Leftrightarrow m^2\ge-3\) (luôn đúng)
Pt có nghiệm với mọi m (đề bài sai)
4.
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x-\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)
6.
ĐKXĐ: \(cosx\ne0\)
Nhân 2 vế với \(cos^2x\)
\(sin^2x-4cosx+5cos^2x=0\)
\(\Leftrightarrow1-cos^2x-4cosx+5cos^2x=0\)
\(\Leftrightarrow\left(2cosx-1\right)^2=0\)
\(\Leftrightarrow cosx=\dfrac{1}{2}\Rightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)

6.
\(cos^2x+\sqrt{3}sinx.cosx-1=0\)
\(\Leftrightarrow-sin^2x+\sqrt{3}sinx.cosx=0\)
\(\Leftrightarrow sinx\left(sinx-\sqrt{3}cosx\right)=0\)
\(\Leftrightarrow sinx\left(\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx\right)=0\)
\(\Leftrightarrow sinx.sin\left(x-\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sin\left(x-\dfrac{\pi}{3}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)


Pt có 2 nghiệm khi: \(\left\{{}\begin{matrix}m\ne0\\\Delta'=9\left(m-1\right)^2-9m\left(m-3\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\m\ge-1\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{6\left(m-1\right)}{m}\\x_1x_2=\dfrac{9\left(m-3\right)}{m}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Rightarrow\dfrac{6\left(m-1\right)}{m}=\dfrac{9\left(m-3\right)}{m}\)
\(\Rightarrow6\left(m-1\right)=9\left(m-3\right)\)
\(\Rightarrow m=7\)
A đúng












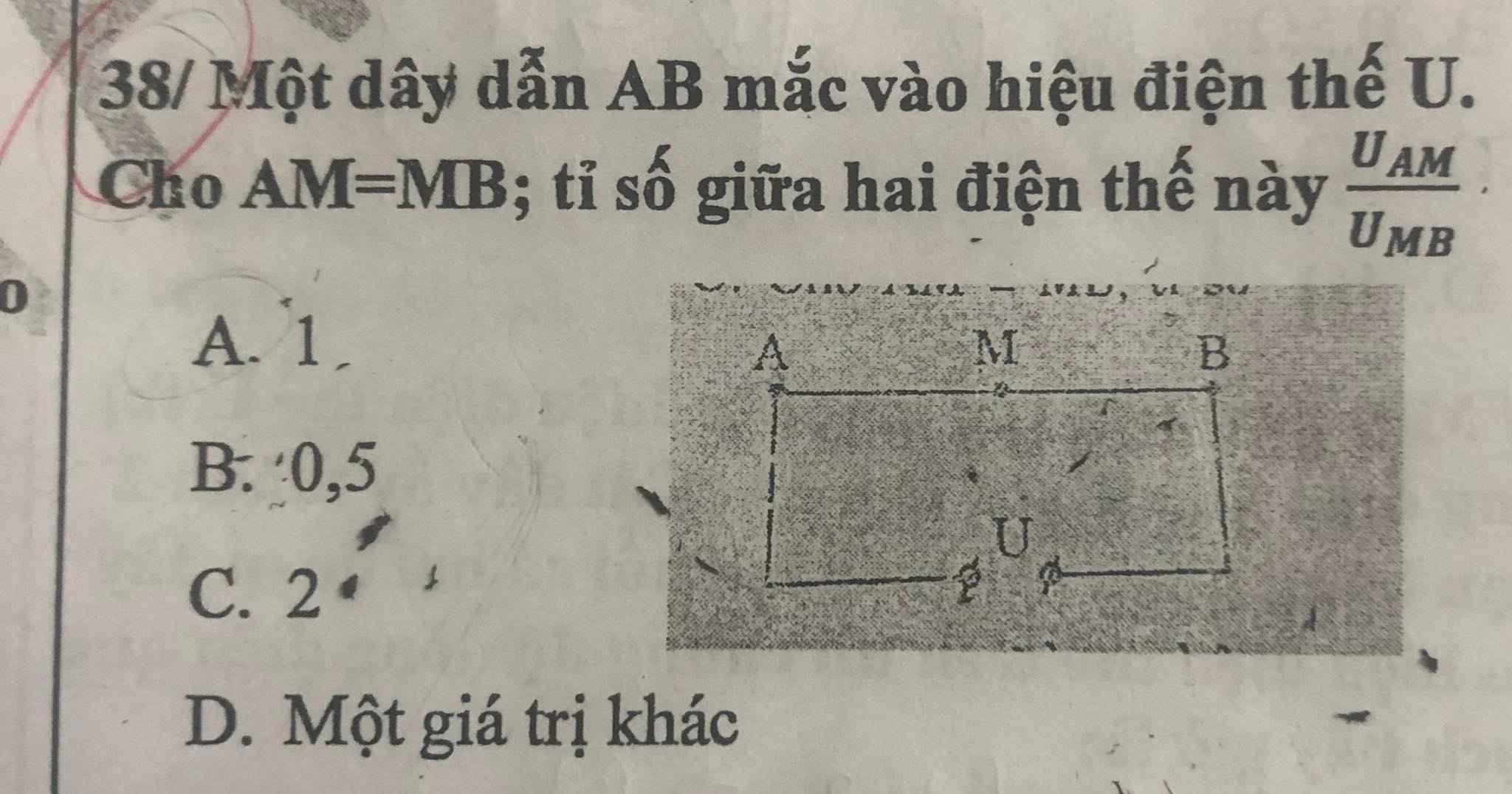
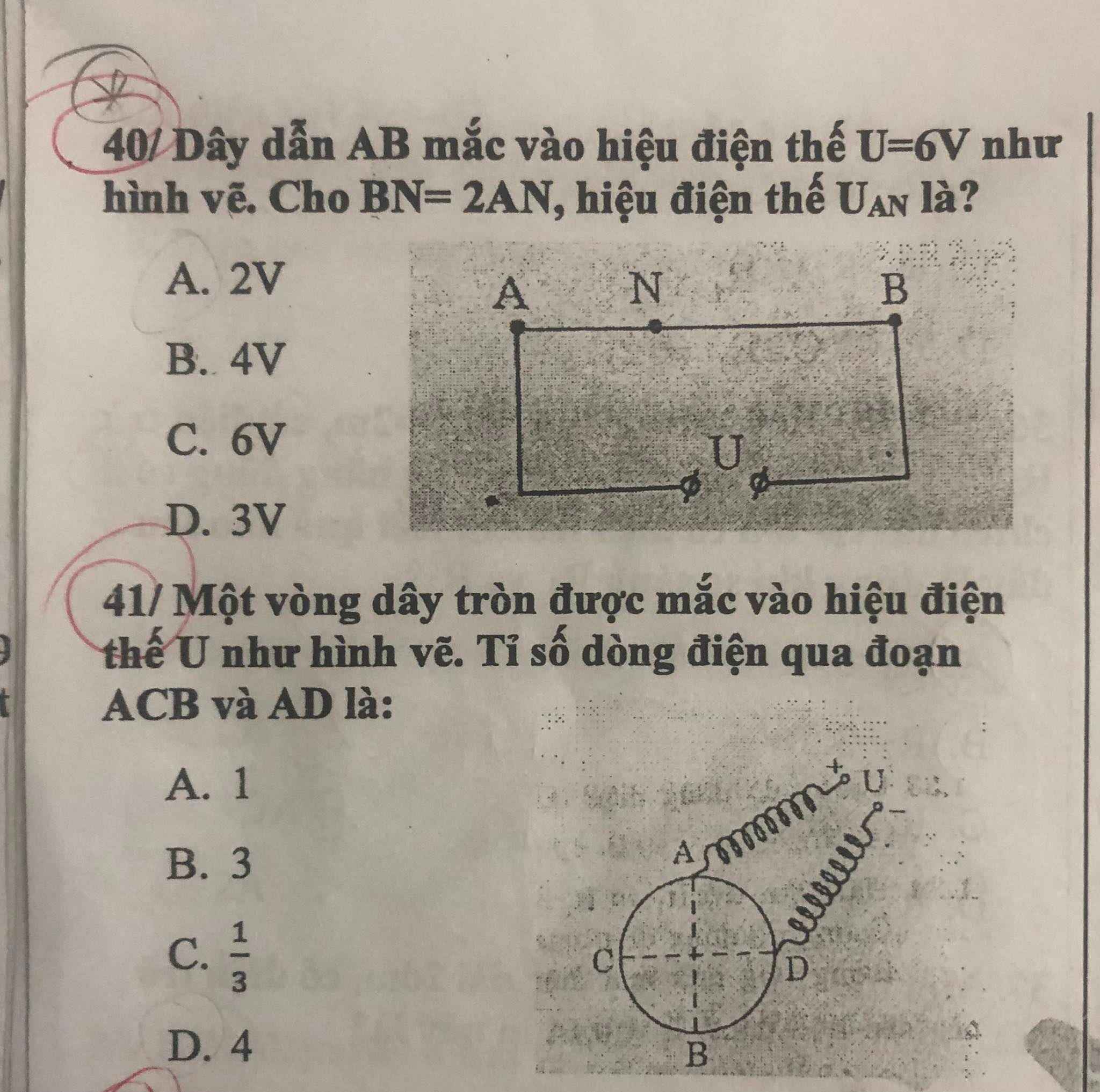
b c b c d d b d b d