Tính giá trị của hàm số tại x = 3, x = – 1, x = 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 9 2018
- Ta có : x = 3 > 2 nên f(3) = 3 + 1 = 4.
- Ta có : x = -1 < 2 nên f(–1) = (-1)2 – 2 = –1.
- Ta có : x = 2 nên f(2) = 2 + 1 = 3.
TM
2
5 tháng 1 2017
=1/2+1/2^2+.....+1/2^100=.................................................................
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Với a = 0, tại x = 4, ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2.0 + 1 = 1\\ \Rightarrow \mathop {\lim }\limits_{x \to 4} f\left( x \right) \ne f\left( 4 \right)\end{array}\)
Do đó hàm số không liên tục tại x = 4.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2a + 1\end{array}\)
Để hàm số liên tục tại x = 4 thì \(\mathop {\lim }\limits_{x \to 4} f\left( x \right) = f\left( 4 \right)\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;21{\rm{ }} = {\rm{ }}2a{\rm{ }} + {\rm{ }}1}\\{ \Leftrightarrow \;2a{\rm{ }} = {\rm{ }}20}\\{ \Leftrightarrow \;a{\rm{ }} = {\rm{ }}10}\end{array}\)
Vậy với a = 10 thì hàm số liên tục tại x = 4.
c) TXĐ: \(\mathbb{R}\)
Với \(x\; \in \;\left( {-{\rm{ }}\infty ;{\rm{ }}4} \right)\) có \(f\left( x \right) = {x^2} + x + 1\) liên tục với mọi x thuộc khoảng này.
Với \(x\; \in \;\left( {4;{\rm{ }} + \infty } \right)\) có \(f\left( x \right) = 2a + 1\) liên tục với mọi x thuộc khoảng này.
Do đó hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) khi hàm số \(f\left( x \right)\) liên tục tại điểm x = 4 khi a = 10.
Vậy với a = 10 hàm số liên tục trên tập xác định của nó.
PT
1
CM
26 tháng 2 2019
f(5) = - 5 2 + 2 . 5 = - 25 + 10 = - 15 vì (5 > 0)
f(-2) = 7/3
f(0) = 3
f(2) = 0
25 tháng 12 2023
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
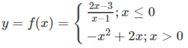
Với x ≥ 2 hàm số có công thức y= f(x) = x + 1.
Vậy giá trị của hàm số tại x = 3 là f(3) = 3 + 1 = 4.
Tương tự, với x < 2 hàm số có công thức y = f(y) = x2 – 2.
Vậy f(- 1) = (- 1)2 – 2 = – 1.
Tại x = 2 giá trị của hàm số là: f(2) = 2 + 1 = 3.
Trả lời: f(3) = 4; f(- 1) = – 1; f(2) = 3