Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(5\right)=-5^2+2.5=-15\)
\(f\left(-2\right)=-\left(-2\right)^2+2.\left(-2\right)=-8\)
\(f\left(2\right)=-2^2+2.2=0\)

Với x ≥ 2 hàm số có công thức y= f(x) = x + 1.
Vậy giá trị của hàm số tại x = 3 là f(3) = 3 + 1 = 4.
Tương tự, với x < 2 hàm số có công thức y = f(y) = x2 - 2.
Vậy f(- 1) = (- 1)2 – 2 = - 1.
Tại x = 2 giá trị của hàm số là: f(2) = 2 + 1 = 3.
Trả lời: f(3) = 4; f(- 1) = - 1; f(2) = 3.

Với x ≥ 2 hàm số có công thức y= f(x) = x + 1.
Vậy giá trị của hàm số tại x = 3 là f(3) = 3 + 1 = 4.
Tương tự, với x < 2 hàm số có công thức y = f(y) = x2 – 2.
Vậy f(- 1) = (- 1)2 – 2 = – 1.
Tại x = 2 giá trị của hàm số là: f(2) = 2 + 1 = 3.
Trả lời: f(3) = 4; f(- 1) = – 1; f(2) = 3

a) Txđ: D =\(\left[1998;+\infty\right]\)
b) \(f\left(2002\right)=620000\) con.
\(g\left(1999\right)=380000\) con.
\(h\left(2000\right)=100000\) con.
c) \(h\left(1999\right)=30000\) con; \(h\left(2002\right)=210000\).
\(h\left(2002\right)-h\left(1999\right)=210000-30000=180000\).
Ý nghĩa: Hiệu \(h\left(2002\right)-h\left(1999\right)\) thể hiện sự tăng trưởng sản lượng ngan qua giai đoạn 1999 - 2002.
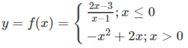


f(5) = - 5 2 + 2 . 5 = - 25 + 10 = - 15 vì (5 > 0)
f(-2) = 7/3
f(0) = 3
f(2) = 0