Cho sin 2a = - và < a < π.Tính sina và...
Đọc tiếp
Cho sin 2a = -
và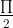 
< a < π.
Tính sina và cosa.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
\(tana=\dfrac{sina}{cosa}=\dfrac{1}{15}\Rightarrow sina=\dfrac{cosa}{15}\)
\(\Rightarrow sin2a=2sina.cosa=\dfrac{2cosa}{15}.cosa=\dfrac{2}{15}cos^2a=\dfrac{2}{15}.\dfrac{1}{1+tan^2a}=\dfrac{2}{15}.\dfrac{1}{1+\dfrac{1}{15^2}}=\dfrac{15}{113}\)
b.
\(5^2=\left(3sina+4cosa\right)^2\le\left(3^2+4^2\right)\left(sin^2+cos^2a\right)=25\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}\dfrac{sina}{3}=\dfrac{cosa}{4}\\3sina+4cosa=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}sina=\dfrac{3}{5}\\cosa=\dfrac{4}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
c.
\(\dfrac{1}{tan^2a}+\dfrac{1}{cot^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)
\(\Leftrightarrow\dfrac{cos^2a}{sin^2a}+\dfrac{sin^2a}{cos^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)
\(\)\(\Leftrightarrow\dfrac{sin^4a+cos^4a}{sin^2a.cos^2a}+\dfrac{sin^2a+cos^2a}{sin^2a.cos^2a}=7\)
\(\Leftrightarrow\dfrac{\left(sin^2a+cos^2a\right)^2-2sin^2a.cos^2a}{sin^2a.cos^2a}+\dfrac{1}{sin^2a.cos^2a}=7\)
\(\Leftrightarrow\dfrac{2}{sin^2a.cos^2a}=9\)
\(\Leftrightarrow\dfrac{8}{\left(2sina.cosa\right)^2}=9\)
\(\Leftrightarrow\dfrac{8}{sin^22a}=9\)
\(\Leftrightarrow sin^22a=\dfrac{8}{9}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vì \(\frac{\pi }{2} < a < \pi \) nên \(\cos a < 0\)
Ta có: \({\sin ^2}a + {\cos ^2}a = 1\)
\(\Leftrightarrow \frac{1}{9} + {\cos ^2}a = 1\)
\(\Leftrightarrow {\cos ^2}a = 1 - \frac{1}{9}= \frac{8}{9}\)
\(\Leftrightarrow \cos a =\pm\sqrt { \frac{8}{9}} = \pm \frac{{2\sqrt 2 }}{3}\)
Vì \(\cos a < 0\) nên \(cos a =-\frac{{2\sqrt 2 }}{3}\)
Suy ra \(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{{\frac{1}{3}}}{{ - \frac{{2\sqrt 2 }}{3}}} = - \frac{{\sqrt 2 }}{4}\)
Ta có: \(\sin 2a = 2\sin a\cos a = 2.\frac{1}{3}.\left( { - \frac{{2\sqrt 2 }}{3}} \right) = - \frac{{4\sqrt 2 }}{9}\)
\(\cos 2a = 1 - 2{\sin ^2}a = 1 - \frac{2}{9} = \frac{7}{9}\)
\(\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}} = \frac{{2.\left( { - \frac{{\sqrt 2 }}{4}} \right)}}{{1 - {{\left( { - \frac{{\sqrt 2 }}{4}} \right)}^2}}} = - \frac{{4\sqrt 2 }}{7}\)
b) Vì \(\frac{\pi }{2} < a < \frac{{3\pi }}{4}\) nên \(\sin a > 0,\cos a < 0\)
\({\left( {\sin a + \cos a} \right)^2} = {\sin ^2}a + {\cos ^2}a + 2\sin a\cos a = 1 + 2\sin a\cos a = \frac{1}{4}\)
Suy ra \(\sin 2a = 2\sin a\cos a = \frac{1}{4} - 1 = - \frac{3}{4}\)
Ta có: \({\sin ^2}a + {\cos ^2}a = 1\;\)
\( \Leftrightarrow \left( {\frac{1}{2} - {\cos }a} \right)^2 + {\cos ^2}a - 1 = 0\)
\( \Leftrightarrow \frac{1}{4} - \cos a + {\cos ^2}a + {\cos ^2}a - 1 = 0\)
\( \Leftrightarrow 2{\cos ^2}a - \cos a - \frac{3}{4} = 0\)
\( \Rightarrow \cos a = \frac{{1 - \sqrt 7 }}{4}\) (Vì \(\cos a < 0)\)
\(\cos 2a = 2{\cos ^2}a - 1 = 2.{\left( {\frac{{1 - \sqrt 7 }}{4}} \right)^2} - 1 = - \frac{{\sqrt 7 }}{4}\)
\(\tan 2a = \frac{{\sin 2a}}{{\cos 2a}} = \frac{{ - \frac{3}{4}}}{{ - \frac{{\sqrt 7 }}{4}}} = \frac{{3\sqrt 7 }}{7}\)
CN
2
5 tháng 6 2020
\(sin^2a+cos^2a-sin^4a-2cos^2a+sin^2a\)
\(=2sin^2a-cos^2a-sin^4a\)
\(=2sin^2a-cos^2a-\left(\frac{1-cos2a}{2}\right)^2\)
khai triển ra rồi quy đồng lên
\(=\frac{8sin^2a-4cos^2a-1+2cos2a-cos^22a}{4}\)
Mà \(2cos2a=2\left(cos^2a-1\right)=4cos^2-2\)
\(\Rightarrow\frac{8sin^2a-cos^22a-3}{4}\)
Mà \(-cos^22a=sin^22a-1=4sin^2cos^2-1\)
\(\Rightarrow\frac{8sin^2a+4sin^2a.cos^2a-4}{4}\)
\(=\frac{4sin^2a.\left(2-cos^2a\right)-4}{4}\)
\(=sin^2a\left(1+sin^2a\right)-1\)
\(=sin^4a-cos^2a\)
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
\(\sin a + \cos a = 1 \Rightarrow {\left( {\sin a + \cos a} \right)^2} = 1 \)
\(\Leftrightarrow {\sin ^2}a + {\cos ^2} + 2\sin a\cos a = 1 \Leftrightarrow 1 + \sin 2a = 1\)
\(\Leftrightarrow \sin 2a = 0\)
DN
20 tháng 9 2017
Câu a dùng sin^2a+cos^2a=1 và a^2-b^2=(a-b)(a+b). Kết quả=sin^2
Câu b tương tự=2
Câu c tách sina ra ngoài và được sin^3a
Câu d dùng hđt a^2+2ab+b^2=(a+b)^2 và kết quả là 1
Câu e tách tan^2a ra ngoài và được tan^2*cos^2 mà tana=sina/cosa. Kết quả bằng sin^2a
Câu f có tan^2*cos^2=sin^2a nên kết quả câu f=1
Chú thích chút ^ là mũ, a là alpha,* là nhân
cos2a =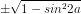
= ±
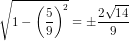
Nếu cos2a =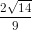
thì
sina =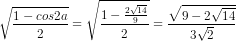
=
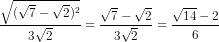
cosa = -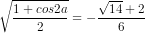
Nếu cos2a = -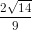
thì
sina =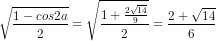
cosa = -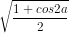
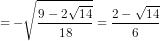
MMẫu giáo thật cơ ạ:))