Một con lắc lò xo gồm một quả nặng m=1kg treo vào một lò xo có độ cứng 1600N/m. Khi quả nặng ở vị trí cân bằng, người ta truyền cho nó một vận tốc ban đầu bằng 2 m/s hướng thẳng xuống dưới.
a) Tính biên độ dao động của quả nặng
b) Viết phương trình dao động của quả nặng. Chọn chiều dương hướng lên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ ω = k m = 1600 1 = 40 rad/s.
+ Truyền cho vật vận tốc 2 m/s tại vị trí cân bằng => vmax = ωA = 2 => A = 0,05m = 5cm.

Tần số góc của dao động
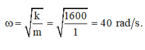
Vận tốc ban đầu chính bằng vận tốc cực đại của dao động
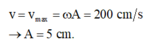
Đáp án A

Đáp án A
+ Tần số góc của dao động ω = k m = 1600 1 = 40 r a d / s
Vận tốc ban đầu chính bằng vận tốc cực đại của dao động v = v m a x = ω A = 200 c m / s → A = 5 c m

Đáp án B
Tần số góc của dao động 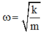
= 40 rad/s
Vận tốc ban đầu cũng chính là vận tốc cực đại
![]()
→ A = 5cm

Chọn đáp án A
Δ l 0 = m g k = 2 , 5 c m ω = k m = 20 → A = x 2 + v 2 ω 2 A = l − Δ l 0 2 + v 2 ω 2 = 2 , 5 2 c m

a) Từ định luật bảo toàn cơ năng ta có:
\(\frac{1}{2}mv^2_0=\frac{1}{2}kA^2\)
\(\Rightarrow A=v_0\sqrt{\frac{m}{k}}=2\sqrt{\frac{1}{1600}}=0,05m=5cm\)
b) Phương trình dao động có dạng: \(x=A\cos\left(\omega t+\varphi\right)\)
Tần số góc: \(\omega=\sqrt{\frac{k}{m}}=\frac{1600}{1}=40rad\text{/s }\)
Tại \(t=0\)\(\begin{cases}x=0=A\cos\varphi\\v=-2=-\omega A\sin\varphi\end{cases}\)\(\Rightarrow\varphi=\frac{\pi}{2}\)
Phương trình dao động: \(x=5\cos\left(40t+\frac{\pi}{2}\right)\left(cm\right)\)
cảm ơn