Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ ω = k m = 1600 1 = 40 rad/s.
+ Truyền cho vật vận tốc 2 m/s tại vị trí cân bằng => vmax = ωA = 2 => A = 0,05m = 5cm.

a) Từ định luật bảo toàn cơ năng ta có:
\(\frac{1}{2}mv^2_0=\frac{1}{2}kA^2\)
\(\Rightarrow A=v_0\sqrt{\frac{m}{k}}=2\sqrt{\frac{1}{1600}}=0,05m=5cm\)
b) Phương trình dao động có dạng: \(x=A\cos\left(\omega t+\varphi\right)\)
Tần số góc: \(\omega=\sqrt{\frac{k}{m}}=\frac{1600}{1}=40rad\text{/s }\)
Tại \(t=0\)\(\begin{cases}x=0=A\cos\varphi\\v=-2=-\omega A\sin\varphi\end{cases}\)\(\Rightarrow\varphi=\frac{\pi}{2}\)
Phương trình dao động: \(x=5\cos\left(40t+\frac{\pi}{2}\right)\left(cm\right)\)

Tần số góc của dao động
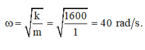
Vận tốc ban đầu chính bằng vận tốc cực đại của dao động
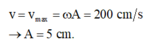
Đáp án A

Chọn chiều + trùng chiều kéo , gốc tọa độ là VTCB .
\(\omega\) =\(\sqrt{\frac{K}{m}}\) = \(\sqrt{40:0,4}\) = 10 rad/s
A = 4 cm
t = 0 :
4 = 4 cos \(\varphi\)
=> cos \(\varphi\) = 1 => \(\varphi\) = 0
x = 4 cos ( 10t )

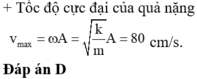
5
áp dụng công thức mối liên hệ giữa vận tốc và li độ
(x^2)/(A^2) + (v^2)/(omega^2*A^2) = 1
mà li độ x=0; v=2
===> A=5cm