Năng lượng của e trong nguyên tử Hidro được viết theo công thức \(En=-A\text{/}n^2\) với \(\text{(n=1,2,3...)}\) Biết bước sóng dài nhất trong dãy Banme do khí H phát ra là 0,6563μm. Xác định bước sóng ngắn nhất trong phổ bức xạ của nt Hidro
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 1 2019
Chọn đáp án C
Ta có
E 1 = − 13 , 6 e V ; E 2 = − 3 , 4 e V ; E 3 = − 1 , 51 e V ; E 4 = − 0 , 85 e V ; E 5 = − 0 , 544 e V
Nhận thấy E 5 − E 2 = − 0 , 544 + 3 , 4 = 2 , 856
→ Khi nguyên tử hấp thụ photon có năng lượng 2,856 eV sẽ chuyển từ trạng thái L lên trạng thái dừng O.
Từ trạng thái O, nguyên tử muốn bức xạ ra photon có bước sóng nhỏ nhất thì nguyên tử phải xuống trạng thái nào đó sao cho hiệu giữa hai mức năng lượng đạt giá trị lớn nhất → nguyên tử chuyển từ trạng thái O về K.
Khi đó ta có
λ = h c E 5 − E 1 = 6 , 625.10 − 34 .3.10 8 − 0 , 544 + 13 , 6 .1 , 6.10 − 19 = 9 , 514.10 − 8 m
VT
16 tháng 1 2019
Đáp án D
Ta có
Nhận thấy
→ Khi nguyên tử hấp thụ photon có năng lượng 2,856 eV sẽ chuyển từ trạng thái L lên trạng thái dừng O.
Từ trạng thái O, nguyên tử muốn bức xạ ra photon có bước sóng nhỏ nhất thì nguyên tử phải xuống trạng thái nào đó sao cho hiệu giữa hai mức năng lượng đạt giá trị lớn nhất → nguyên tử chuyển từ trạng thái O về K.
Khi đó ta có
VT
13 tháng 1 2019
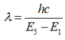
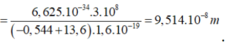
+ Theo tiên đề Bo thứ II ta có:
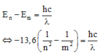
+ Áp dụng cho quá trình từ n = 5 về n = 4 ta có:
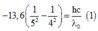
+ Áp dụng cho quá trình từ n = 4 về n = 2 ta có:
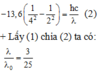
=> Chọn B.
HD
Hà Đức Thọ
Admin
19 tháng 2 2016
Bước sóng dài nhất trong dãy Ban me khi nguyên tử chuyển từ mức 3 về 2 --> \(\dfrac{hc}{\lambda_{32}}=E_3-E_2=-\dfrac{13,6eV}{3^2}+\dfrac{13,6eV}{2^2}\) --> \(\lambda _{32}\)
Bước sóng ngắn nhất trong dãy pasen khi nguyên tử chuyển từ mức vô cùng về 3 --> \(\dfrac{hc}{\lambda}=E_n-E_3=0+\dfrac{13,6eV}{3^2}\)--> \(\lambda\)
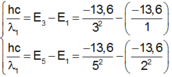
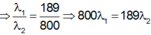
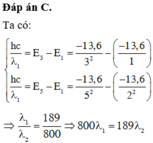
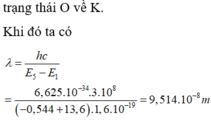
Bước sóng dài nhất trong quang phổ Banmel sẽ là bước sóng ứng với bước chuyển từ 3 xuống 2
\(E=\frac{hc}{\lambda}=E_3-E_2=A\text{/}4-A\text{/}9\)
\(\Rightarrow A=2,18.10^{-19}J\)
Mình không hiểu câu hỏi của bạn lắm nhưng theo mình đoán bước sóng ngắn nhất này sẽ từ \(\text{n=∞ }\)
đến n=1
Năng lượng sẽ đúng bằng A
\(\lambda=\text{91,1528nm }\)