Cho tam giác ABC có góc A=90 độ, AB=AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA tại K. CMR AK=AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HL
12 tháng 11 2022
Xét tam giác BKE có: KG và BA là các đường cao => ED cũng là đường cao => ED vuông góc với BK.
Vì tam giác ABC vuông cân, AD = AE => DE //BC và góc ABC = 45 độ
=> BC vuông gocsvowis BK (vì DE vuông góc BK, BC // DE)
=> góc CBK = 90 độ => góc ABK = góc CBA - góc CBA = 90 - 45= 45.
Tam giác BKC có BA vừa là đường cao, vừa là phân giác => BKC cân => AC = AK (đpcm)
HN
5 tháng 6 2017
Xét hai tam giác KAD và BAE có:
\(\widehat{KAD}=\widehat{BAE}\left(=90^o\right)\)
AD = AE (gt)
\(\widehat{D_1}=\widehat{E_1}\) (cùng phụ với góc K)
Vậy: \(\Delta KAD=\Delta BAE\left(g-c-g\right)\)
Suy ra: AK = AB (hai cạnh tương ứng)
Ta lại có AB = AC
Do đó: AK = AC.
HK
28 tháng 8 2021
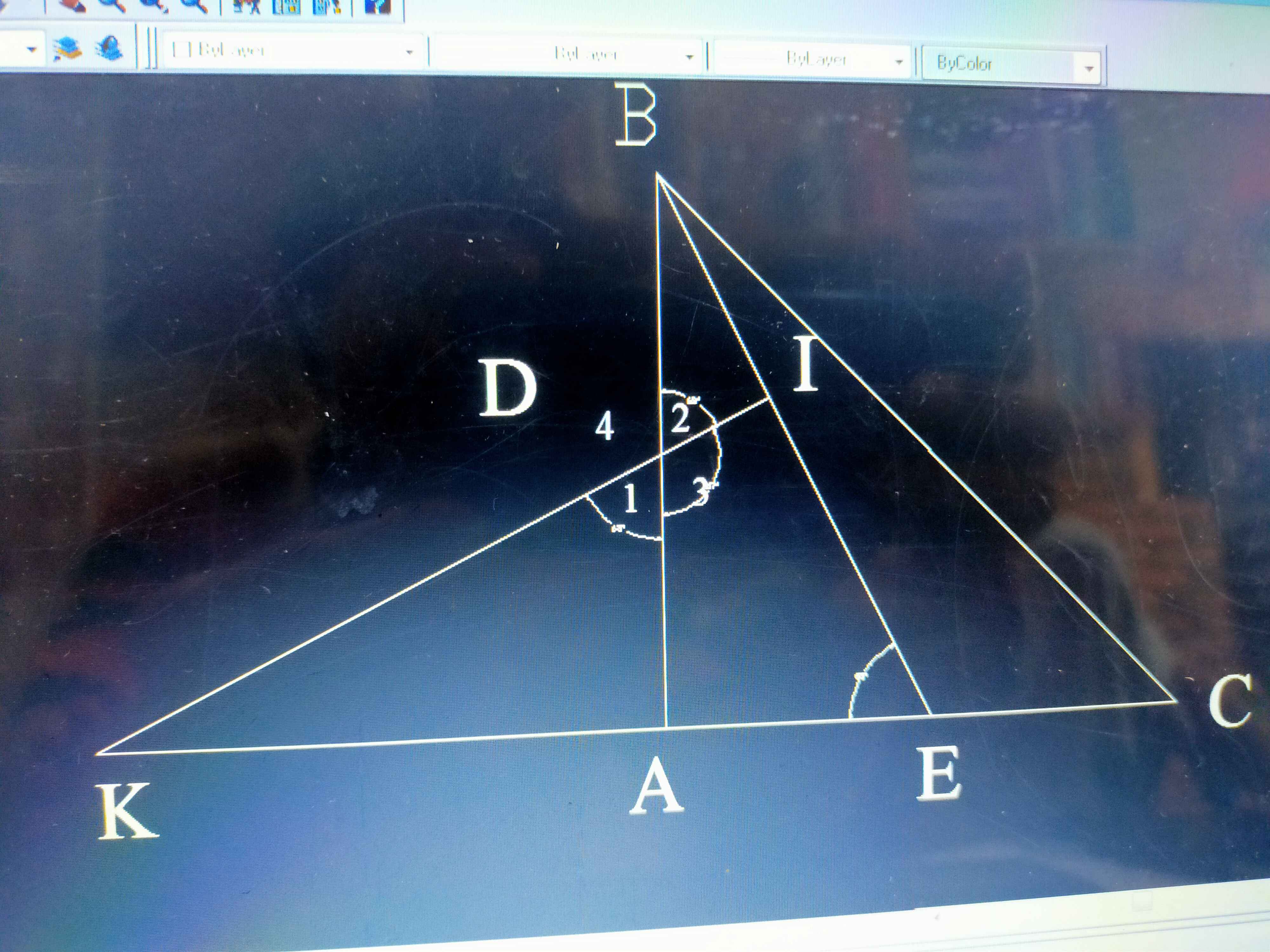Xet tứ giác ADIE ta có: góc D3+ E =180
> D3=180- E.
> D4=180-D1
[ Góc D3 =D4 (đối đỉnh)]
>> góc D1= E.
xét tam giác ABE và tam giác KAD. Có góc D1=E, cạnh AD=AE,
---> Tam giác ABE = tam giác KAD.
-->> AB =AK
> AB=AC=KA
AK=AC.
>>
Xét tam giác BKE có: KG và BA là các đường cao => ED cũng là đường cao => ED vuông góc với BK.
Vì tam giác ABC vuông cân, AD = AE => DE //BC và góc ABC = 45 độ
=> BC vuông gocsvowis BK (vì DE vuông góc BK, BC // DE)
=> góc CBK = 90 độ => góc ABK = góc CBA - góc CBA = 90 - 45= 45.
Tam giác BKC có BA vừa là đường cao, vừa là phân giác => BKC cân => AC = AK (đpcm)