Các cao thủ giúp em bài này: Một con lắc đơn khi dao động với biên độ góc α1 = 30 thì lực căng dây lúc gia tốc cực tiểu là T1, khi dao động với biên độ góc α2 = 60 thì lực căng dây lúc gia tốc cực tiểu là T2. Tỉ số T2/T1 là? (Đáp /án 0,78) . Em cảm ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lực căng dây nhỏ nhất ở vị trí biên
T m i n = mgcos α 0
Lực căng dây lớn nhất ở vị trí cân bằng
T m a x - mg = m v 2 m a x /l ⇒ T m a x = mg + m v 2 m a x /l
Mặt khác cơ năng của con lắc là
W = 1/2 .m v 2 m a x = 1/2 .mgl α 0 2
⇒ m v 2 m a x /l = mg α 0 2
⇒ T m a x = mg(l + α 0 2 )
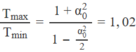
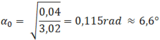

Đáp án D
+ Biểu thức tính lực căng dây của con lắc đơn T = mg(3cosα – 2cos α o ).

Đáp án A
+ Lực căng dây của con lắc T = mg 3 cosα − 2 cosα 0 → α = α 0 T = mgcosα 0
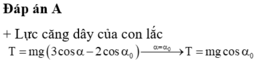
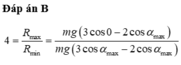
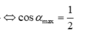
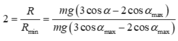
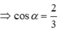

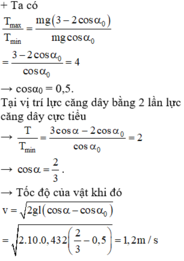
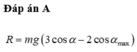
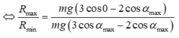
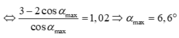
Gia tốc trong dao động của con lắc đơn gồm 2 thành phần: tiếp tuyến + hướng tâm.
Giả sử biên độ góc là \(\alpha_0\), để tìm gia tốc khi biên độ góc là \(\alpha\le\alpha_0\) ta làm như sau:
+ Gia tốc hướng tâm: \(a_{ht}=\frac{v^2}{l}=\frac{2gl\left(\cos\alpha-\cos\alpha_0\right)}{l}=2g\left(\cos\alpha-\cos\alpha_0\right)\)
+ Gia tốc tiếp tuyến: \(a_{tt}=\frac{F_{tt}}{m}=g\sin\alpha\)
+ Gia tốc là a \(\Rightarrow a^2=a_{ht}^2+a_{tt}^2=g\left[4\left(\cos\alpha-\cos\alpha_0\right)^2+\sin^2\alpha\right]\)\(=g\left[3\cos^2\alpha-8\cos\alpha_0\cos\alpha+1\right]\)
Suy ra a min khi \(\cos\alpha=\frac{4}{3}\cos\alpha_0\)
Khi đó, lực căng dây là: \(\tau=mg\left(3\cos\alpha-2\cos\alpha_0\right)=2mg\cos\alpha_0\)
Tỉ số lực căng dây: \(\frac{\tau_2}{\tau_1}=\frac{\cos\alpha_2}{\cos\alpha_1}=\frac{\cos60^0}{\cos30^0}=0,58\)