Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ hệ thức độc lập thời gian giữa li độ dài và vận tốc:
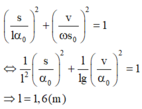
Đáp án C

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Đáp án D
Thời điểm ban đầu con lắc đang ở vị trí có li độ α = α 0 2 và đang chuyển động theo chiều âm ⇒ φ 0 = π 3
Áp dụng công thức độc lập giữa biên độ dài, li độ và vận tốc, ta có:
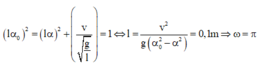

Li độ dài ban đầu của nó là:
$x=\alpha.l=2$cm
Có: $\omega^2=\frac{g}{l}$
Áp dụng công thức liên hệ giữa li độ và vận tốc trong dao động điều hoà ta có:
$A^2=x^2+\frac{v^2}{\omega^2}$
$\Rightarrow A=2\sqrt2$cm
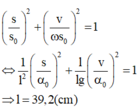

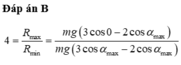
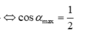
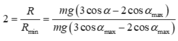
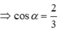

Đáp án B