Một chất điểm DĐĐH trên trục X'OX với phương trình x=10cos(pi.t)(cm). Thời điểm vật đi qua li độ x=+5cm theo chiều âm lần thứ hai kể từlúc dao động?
Giải thích cụ thể giúp mình nhé.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
@ Lời giải:
![]()
+ Ban đầu vật ở biên dương
+ Vị trí vật có li độ x = -4cm ngược chiều dương ứng với góc 1200
+ Thời gian vật đi qua vị trí x = -4cm theo chiều dương lần thứ 2 là:
![]()

Chu kỳ T = 2π/ω=0,2s
Ban đầu vật ở biên dương
Vị trí vật có li độ x = -4cm ngược chiều dương ứng với góc 120 độ
Thời gian vật đi qua vị trí x = -4cm theo chiều dương lần thứ 2 là:t=T/3 + T=4/15s
Chọn đáp án B

Đáp án A
Phương pháp: Khoảng cách giữa hai điểm sáng được biểu diễn bởi phương trình:
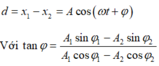
Sử dụng đường tròn lượng giác
Cách giải:
+ Phương trình vận tốc của hai chất điểm:
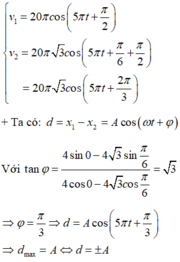
+ Thời điểm đầu tiên t hai điểm sáng cách xa nhau nhất được biểu diễn trên đường tròn lượng giác:
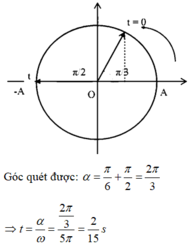
+ Tại t = 2/15s tỉ số vận tốc của chất điểm 1 so với chất điểm 2:
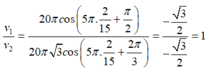

Phương pháp: Khoảng cách giữa hai điểm sáng được biểu diễn bởi phương trình:
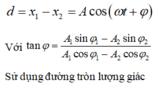
Cách giải:
+ Phương trình vận tốc của hai chất điểm:
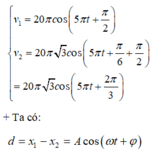
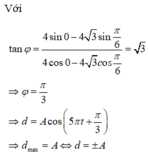
+ Thời điểm đầu tiên t hai điểm sáng cách xa nhau nhất được biểu diễn trên đường tròn lượng giác
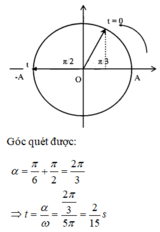
+ Tại t = 2/15s tỉ số vận tốc của chất điểm 1 so với chất điểm 2:
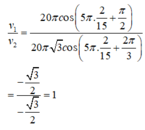
Đáp án A

Chọn đáp án D
@ Lời giải:
+ Thế năng của vật dao động điều hòa biến thiên tuần hoàn với tần số góc:
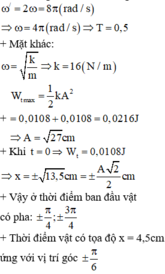
+ Vậy thời điểm vật qua vị trí x = 4,5cm lần đầu tiên là: T 24 = 1 48 s

Lời giải:
Vì tại thời điểm ban đầu vật đang qua VTCB theo chiều âm nên phương trình dao động của vật \(x=A\cos\left(\omega t+\frac{\pi}{2}\right)\) (cm)
Từ điều kiện đề bài kết hợp với công thức \(A^2=x^2+\left(\frac{v}{\omega}\right)^2\) nên \(\omega=2\pi\Rightarrow A=5\left(cm\right)\)
Do đó phương trình là \(x=5\cos\left(2\pi t+\frac{\pi}{2}\right)\left(cm\right)\)
Biểu diễn dao động bằng véc tơ quay như hình vẽ. Vật qua li độ 5cm theo chiều âm --> véc tơ quay qua N.
Lần thứ 2 --> véc tơ xuất phát từ M (ban đầu), quay hết 1 vòng rồi quay tiếp đến N
Thời gian: \(t=T+\frac{60}{360}T=\frac{7}{6}T=\frac{7}{6}.2=\frac{7}{3}s\)
A