Có đáp án là C. nhưng em chưa biết cách giải. mọi người giải chi tiết giúp em nhé.Câu 1: Cho ba vật dao động điều hòa cùng biên độ A = 10cm nhưng tần số khác nhau. Biết rằng tại mọi thời điểm, li độ, vận tốc của các vật liên hệ với nhau bởi biểu thức: \(\frac{x1}{v1}+\frac{x2}{v2}=\frac{x3}{v3}\).Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6cm; 8cm và x0. Giá trị...
Đọc tiếp
Có đáp án là C. nhưng em chưa biết cách giải. mọi người giải chi tiết giúp em nhé.
Câu 1: Cho ba vật dao động điều hòa cùng biên độ A = 10cm nhưng tần số khác nhau. Biết rằng tại mọi thời điểm, li độ, vận tốc của các vật liên hệ với nhau bởi biểu thức: \(\frac{x1}{v1}+\frac{x2}{v2}=\frac{x3}{v3}\).Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6cm; 8cm và x0. Giá trị x0 gần giá trị nào nhất trong các giá trị sau:
A. 7,8cm B. 9,0cm C. 8,7cm D. 8,5cm
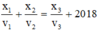. Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6 cm, 8 cm và
x
3
. Giá trị
x
3
. Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6 cm; 8 cm và
x
0
. Giá trị
x
0
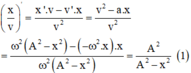
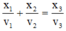
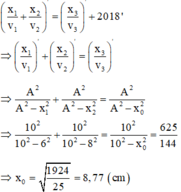
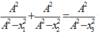
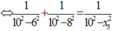
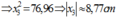
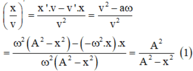
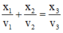
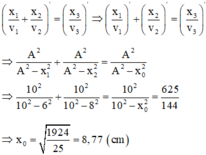
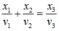
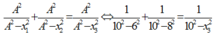
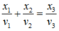
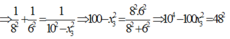
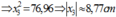
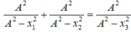
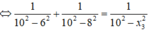
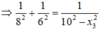
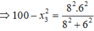
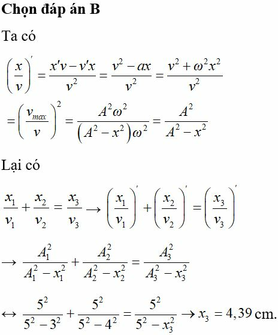
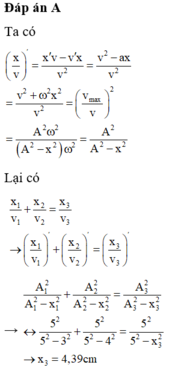
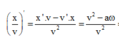
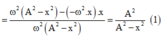
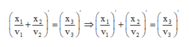
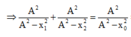
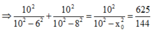
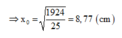
Ta có: \(\left(\frac{v}{x}\right)'=\frac{v^2-ax}{v^2}\)
Mà: \(a=-\omega^2x\) nên \(\left(\frac{v}{x}\right)'=1+\frac{\omega^2x}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế biểu thức đã cho ta có:
\(1+\frac{x_1^2}{A^2-x_1^2}+1+\frac{x_2^2}{A^2-x_2^2}=1+\frac{x_3^2}{A^2-x_3^2}\)
Thay số vào ta tìm đc giá trị \(x_0\)
Em hiểu thế này có đúng không ạ? Tại em biến đổi phương trình đầu tiên của nhưng mà không có ra?
\((\frac{x}{v})' = \frac{x'.v - v'.x}{v^2}= \frac{v^2-ax}{v^2}\)
hay là
\((\frac{v}{x})'= \frac{ax - x^2}{v^2}\)