(X-1/2)^2 =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 7 2023
a, (\(x-2\))2 - (2\(x\) + 3)2 = 0
(\(x\) - 2 - 2\(x\) - 3)(\(x\) - 2 + 2\(x\) + 3) = 0
(-\(x\) - 5)(3\(x\) +1) = 0
\(\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-5\\3x=-1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-5\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(x\in\) { -5;- \(\dfrac{1}{3}\)}
b, 9.(2\(x\) + 1)2 - 4.(\(x\) + 1)2 = 0
{3.(2\(x\) + 1) - 2.(\(x\) +1)}{ 3.(2\(x\) +1) + 2.(\(x\) +1)} = 0
(6\(x\) + 3 - 2\(x\) - 2)(6\(x\) + 3 + 2\(x\) + 2) = 0
(4\(x\) + 1)(8\(x\) + 5) =0
\(\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{5}{8}\end{matrix}\right.\)
S = { - \(\dfrac{5}{8}\); \(\dfrac{-1}{4}\)}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 7 2023
d, \(x^2\)(\(x\) + 1) - \(x\) (\(x+1\)) + \(x\)(\(x\) -1) = 0
\(x\left(x+1\right)\).(\(x\) - 1) + \(x\)(\(x\) -1) = 0
\(x\)(\(x\) -1)(\(x\) + 1 + 1) = 0
\(x\left(x-1\right)\left(x+2\right)\) = 0
\(\left[{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)
S = { -2; 0; 1}
7 tháng 8 2018
1)x^2-2x-1=0
<=> (x^2-2x+1)-2=0
<=>(x-1)2 =2
=>x-1 = \(\pm\sqrt{2}\)
=> x= \(\pm\sqrt{2}\) +1
2) x^2-x-1=0
<=> (x^2-x+1/4) -5/4=0
<=>(x+1/2)2= 5/4
=> x+1/2 = \(\pm\sqrt{\dfrac{5}{4}}\)
=>x=\(\pm\sqrt{\dfrac{5}{4}}\) - 1/2
7 tháng 8 2018
3)x^2+x-3=0
<=> (x^2 + x + 1/4) -13/4=0
<=>(x+1/2)2 = 13/4
=> x+1/2 = \(\sqrt{\dfrac{13}{4}}\)
=> x= \(\sqrt{\dfrac{13}{4}}\) -1/2
4) 4x^2-4x-1=0
<=> (4x^2-4x+1)-2=0
<=>(2x-1)2 -2=0
<=> (2x-1)2 - \(\left(\sqrt{2}\right)^2\) =0
<=> (2x-1 - \(\sqrt{2}\) ) . (2x-1 +\(\sqrt{2}\) )=0
=> 2x-1-\(\sqrt{2}\) =0 hoặc 2x-1+\(\sqrt{2}\) =0
=> 2x= 1+\(\sqrt{2}\) hoặc 2x= 1 - \(\sqrt{2}\)
=> x=\(\dfrac{1+\sqrt{2}}{2}\) hoặc x=\(\dfrac{1-\sqrt{2}}{2}\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
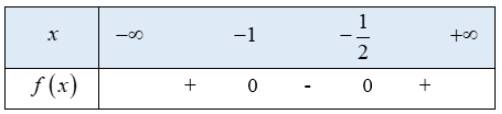
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:
Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
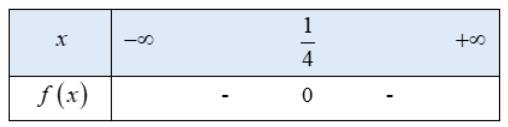
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)
ND
Nguyễn Đức Trí
VIP
18 tháng 7 2023
a)\(\left(x-2\right)^2-\left(2x+3\right)^2=0\Rightarrow\left(x-2+2x+3\right)\left(x-2-2x-3\right)=0\)
\(\Rightarrow\left(3x+1\right)\left(-x-5\right)=0\Rightarrow\left[{}\begin{matrix}3x+1=0\\-x-5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-5\end{matrix}\right.\)
b)\(9\left(2x+1\right)^2-4\left(x+1\right)^2=0\Rightarrow\left[3\left(2x+1\right)+2\left(x+1\right)\right]\left[3\left(2x+1\right)-2\left(x+1\right)\right]=0\)
\(\Rightarrow\left[8x+5\right]\left[4x+1\right]=0\Rightarrow\left[{}\begin{matrix}8x+5=0\\4x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{8}\\x=\dfrac{1}{4}\end{matrix}\right.\)
c)\(x^3-6x^2+9x=0\Rightarrow x\left(x^2-6x+9\right)=0\Rightarrow x\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
d) \(x^2\left(x+1\right)-x\left(x+1\right)+x\left(x-1\right)=0\)
\(\Rightarrow x\left(x+1\right)\left(x^2-1\right)+x\left(x-1\right)=0\)
\(\Rightarrow x\left(x+1\right)\left(x-1\right)\left(x+1\right)+x\left(x-1\right)=0\)
\(\Rightarrow x\left(x-1\right)\left[\left(x+1\right)\left(x+1\right)+1\right]=0\)
\(\Rightarrow x\left(x-1\right)\left[\left(x+1\right)^2+1\right]=0\)
Do \(\left(x+1\right)^2+1>0\)
\(\Rightarrow x\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
MA
3
30 tháng 9 2016
\(x^2-25+2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-5\right)+2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-5+2\right)=0\)
\(\left(x+5\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=3\end{cases}}}\)
20 tháng 1 2018
\(x\left(x-1\right)+x-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+1=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
P/s tham khảo nha
8 tháng 3 2021
a) Ta có: \(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)hay x=1
Vậy: S={1}
c) Ta có: \(x+x^4=0\)
\(\Leftrightarrow x\left(x^3+1\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x^2-x+1\right)=0\)
mà \(x^2-x+1>0\forall x\)
nên x(x+1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy: S={0;-1}
19 tháng 4 2020
Giúp luôn Đức Hải Nguyễn câu e:
e, (x - 1)2 + 2(x - 1)(x + 2) + (x + 2)2 = 0
\(\Leftrightarrow\) (x - 1 + x + 2)2 = 0
\(\Leftrightarrow\) (2x + 1)2 = 0
\(\Leftrightarrow\) 2x + 1 = 0
\(\Leftrightarrow\) x = \(\frac{-1}{2}\)
Vậy S = {\(\frac{-1}{2}\)}
Chúc bn học tốt!!
LT
19 tháng 4 2020
a) (x - 3)(5 - 2x) = 0
<=> \(\left[{}\begin{matrix}x-3=0\\5-2x=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=3\\x=\frac{5}{2}\end{matrix}\right.\)
b) (x + 5)(x - 1) - 2x(x - 1) = 0
<=> (x - 1)(x + 5 - 2x) = 0
<=> (x - 1)(5 - x) = 0
<=> \(\left[{}\begin{matrix}x-1=0\\5-x=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
c) 5(x + 3)(x - 2) - 3(x + 5)(x - 2) = 0
<=> (x - 2)[5(x + 3) - 3(x + 5)] = 0
<=> (x - 2)(5x + 3 - 3x - 15) = 0
<=> (x - 2)(2x - 12) = 0
<=> \(\left[{}\begin{matrix}x-2=0\\2x-12=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)
d) (x - 6)(x + 1) - 2(x + 1) = 0
<=> (x + 1)(x - 6 - 2) = 0
<=> (x + 1)(x - 8) = 0
<=> \(\left[{}\begin{matrix}x+1=0\\x-8=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=-1\\x=8\end{matrix}\right.\)
Câu e thì để mình nghĩ đã :)
#Học tốt!
1 tháng 3 2020
a) 3x(x - 1) + 2(x - 1) = 0
<=> (3x + 2)(x - 1) = 0
<=> \(\orbr{\begin{cases}3x+2=0\\x-1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-\frac{2}{3}\\x=1\end{cases}}\)
Vậy S = {-2/3; 1}
b) x2 - 1 - (x + 5)(2 - x) = 0
<=> x2 - 1 - 2x + x2 - 10 + 5x = 0
<=> 2x2 + 3x - 11 = 0
<=> 2(x2 + 3/2x + 9/16 - 97/16) = 0
<=> (x + 3/4)2 - 97/16 = 0
<=> \(\orbr{\begin{cases}x+\frac{3}{4}=\frac{\sqrt{97}}{4}\\x+\frac{3}{4}=-\frac{\sqrt{97}}{4}\end{cases}}\)
<=> \(\orbr{\begin{cases}x=\frac{\sqrt{97}-3}{4}\\x=-\frac{\sqrt{97}-3}{4}\end{cases}}\)
Vậy S = {\(\frac{\sqrt{97}-3}{4}\); \(-\frac{\sqrt{97}-3}{4}\)
d) x(2x - 3) - 4x + 6 = 0
<=> x(2x - 3) - 2(2x - 3) = 0
<=> (x - 2)(2x - 3) = 0
<=> \(\orbr{\begin{cases}x-2=0\\2x-3=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=2\\x=\frac{3}{2}\end{cases}}\)
Vậy S = {2; 3/2}
e) x3 - 1 = x(x - 1)
<=> (x - 1)(x2 + x + 1) - x(x - 1) = 0
<=> (x - 1)(x2 + x + 1 - x) = 0
<=> (x - 1)(x2 + 1) = 0
<=> x - 1 = 0
<=> x = 1
Vậy S = {1}
f) (2x - 5)2 - x2 - 4x - 4 = 0
<=> (2x - 5)2 - (x + 2)2 = 0
<=> (2x - 5 - x - 2)(2x - 5 + x + 2) = 0
<=> (x - 7)(3x - 3) = 0
<=> \(\orbr{\begin{cases}x-7=0\\3x-3=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=7\\x=1\end{cases}}\)
Vậy S = {7; 1}
h) (x - 2)(x2 + 3x - 2) - x3 + 8 = 0
<=> (x - 2)(x2 + 3x - 2) - (x- 2)(x2 + 2x + 4) = 0
<=> (x - 2)(x2 + 3x - 2 - x2 - 2x - 4) = 0
<=> (x - 2)(x - 6) = 0
<=> \(\orbr{\begin{cases}x-2=0\\x-6=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=2\\x=6\end{cases}}\)
Vậy S = {2; 6}
1 tháng 3 2020
\(a,3x\left(x-1\right)+2\left(x-1\right)=0\)
\(3x.x-3x+2x-2=0\)
\(2x-2=0\)
\(2x=2\)
\(x=1\)
(X-1/2)^2 =0
=>x-1/2=0
=>x=1/2
Vậy x=1/2
Học tốt:33
(x−12)2=0(x−12)2=0
x−12=0x−12=0
x=12x=12
b.Vì: (x−3)2≥0∀x(x−3)2≥0∀x
Mà:(x−3)2=−1(x−3)2=−1 => vô lí
=> ko cs gt của x thỏa mãn