Đường thẳng d qua M (4; 1) và cắt các tia Ox, Oy lần lượt tại A và B sao cho tổng OA + OB nhỏ nhất. Viết phương trình đường thẳng d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 12 2021
\(a,\Leftrightarrow A\left(0;0\right)\in\left(d\right)\Leftrightarrow-2m+1=0\Leftrightarrow m=\dfrac{1}{2}\\ b,\Leftrightarrow x=3;y=4\Leftrightarrow3\left(m+1\right)-2m+1=4\\ \Leftrightarrow3m+3-2m+1=4\\ \Leftrightarrow m=0\Leftrightarrow\left(d\right):y=x+1\\ c,\text{PT hoành độ giao điểm: }x+1=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow B\left(1;2\right)\\ \text{Vậy }B\left(1;2\right)\text{ là giao 2 đths}\)
14 tháng 1
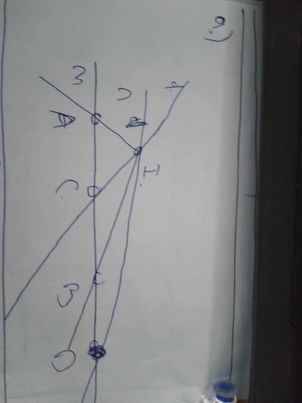
b: Các tia gốc B là Bm,BD
Trục đối xứng của hình chữ nhật ABCD là MN,EF
Tâm đối xứng của hình chữ nhật ABCD là O
CM
5 tháng 11 2018
-Đường thẳng a là đường thẳng số 2
-Đường thẳng b là đường thẳng số 1
-Đường thẳng c là đường thẳng số 3
-Đường thẳng d là đường thẳng số 4
AT
31 tháng 5 2021
a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)
23 tháng 2 2023
a: Vì Δ//d nên Δ: 3x-4y+c=0
Thay x=1 và y=4 vào Δ, ta được:
c+3-16=0
=>c=13
b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0
Thay x=-3 và y=-5 vào Δ, ta được:
c+4*(-3)+3(-5)=0
=>c-27=0
=>c=27
=>4x+3y+27=0
DD
8 tháng 4 2020
a) Để đường thẳng (d) đi qua gốc tọa độ thì m + 1 = 0 => m = 1
Vậy m=1 thì đường thẳng (d) đi qua gốc tọa độ
b) Thay x = 3; y = 4 vào đường thẳng (d) ta được:
4 = (m + 1).3 - 2m + 1
<=> 3m + 3 -2m +1 - 4 = 0
<=> m = 0
Vậy m = 0 thì đường thẳng (d) đi qua điểm A(3;4)
Sorry vì mik ko vẽ được đồ thị cho bạn
c) Đường thẳng vừa vẽ được: y = x + 1
Phương trình hoành độ giao điểm của đường thẳng y = x + 1 và đường thẳng y = -2x + 4 là:
x + 1 = -2x + 4
<=> x + 2x = 4 - 1
<=> 3x = 3
<=> x = 1
Tung độ của 2 đường thẳng y = x + 1 và đường thẳng y = -2x + 4 là:
y = 1 + 1
<=> y = 2
Vậy tọa độ giao điểm của đường thẳng y = x + 1 và đường thẳng y = -2x + 4 là (1;2)
Học tốt. Nhớ k cho mik nha.
10 tháng 4 2020
Lời giải:
P/s: Làm nhưng k biết có đúng hay không!!! (^-^)
Gọi giao điểm mà đồ thị hàm số (y) cắt trục tung là A
Theo bài ra ta có hoành độ của A là 1
Vì A nằm trên trục tung nên hoành độ của A là 0
Do đó điểm A = ( 0 , 1 )
A thuộc đồ thị hàm số (y) nên: ⇒ (m+1)x -2m+1(d)\(\Rightarrow\)m = − 2
~Học tốt!~
CM
23 tháng 9 2017
Gọi phương trình đường thẳng d cần tìm là y = a x + b ( a ≠ 0 )
Vì d // d’ nên a = − 2 b ≠ − 5 ⇒ d: y = − 2 x + b
Thay tọa độ điểm M vào phương trình đường thẳng d ta được:
− 2 . ( − 1 ) + b = 4 ⇒ b = 2 (thỏa mãn)
Vậy phương trình đường thẳng d: y = − 2 x + 2
Đáp án cần chọn là: C
LV
31 tháng 10 2021
a, kẻ đoạn AB bằng thước 4cm
gọi I là trung điểm AB , từ I kẻ đường thẳng d vuông góc vs AB , ta dc d là đường trung trực của AB
b, gọi M là điểm thuộc d , VẼ
c, Vì ta có AB vuông góc vs d mà a song song vs AB
suy ra a vuông góc vs đường thẳng d
Do d cắt 2 trục, gọi pt d có dạng: \(y=ax+b\) (\(a\ne0\))
d đi qua M nên: \(4a+b=1\Rightarrow b=-4a+1\Rightarrow y=ax-4a+1\)
Hoành độ A là nghiệm: \(ax_A-4a+1=0\Rightarrow x_A=\dfrac{4a-1}{a}\)
Tung độ B là nghiệm: \(y_A=a.0-4a+1=-4a+1\)
Do A; B nằm trên các tia Ox, Oy \(\Rightarrow\left\{{}\begin{matrix}\dfrac{4a-1}{a}>0\\-4a+1>0\end{matrix}\right.\) \(\Rightarrow a< 0\)
Khi đó ta có: \(\left\{{}\begin{matrix}OA=x_A=\dfrac{4a-1}{a}\\OB=y_A=-4a+1\end{matrix}\right.\)
\(S=OA+OB=\dfrac{4a-1}{a}-4a+1=5+\left(-4a+\dfrac{1}{-a}\right)\ge5+2\sqrt{\dfrac{-4a}{-a}}=9\)
\(S_{min}=9\) khi \(-4a=\dfrac{1}{-a}\Leftrightarrow a=-\dfrac{1}{2}\)
Phương trình d: \(y=-\dfrac{1}{2}x+3\)