cho hai góc xoy và x’oy’ tnoar nãm ox//ox’ và oy//oy’.chứng minh góc xoy = góc x’oy’ hoặc góc xoy+ góc x’oy’=180độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 7 2019
a) Ta có :
xOy' + y'Ox' =90 độ (gt)
y'Ox' + x'Oy = 90 độ (gt)
=> xOy' = 90 - y'Ox'
=> x'Oy = 90 - y'Ox'
=> xOy' = x'Oy (cùng bằng 90 - y'Ox')(dpcm)
1 tháng 7 2019
b) Gọi Ot là pg y'Ox'(1)
=> y'Ot = x'Ot
tOy = tOx' + x'Oy
Mà y'Ot = tOx'
xOy' = x'Oy (cmt)
=> xOt = tOy
=> Ot là pg xOy (2)
Từ (1) và (2) ta có :
=> y'Ox' và xOy có cùng tia pg
10 tháng 9 2019
Cmr + vẽ hình
Gọi A là giao điểm của Ox và Oy
=> Ta có:
\(\widehat{xOy}=\widehat{OAO'}\left(slt\right)\)
\(OAO=\widehat{xO''A}\left(slt\right)\)
Vậy đã chứng minh xong \(\widehat{xOy}=\widehat{xOy'}\)
11 tháng 9 2019
Sửa đề : Cho góc nhọn xOy và 1 điểm O'.Hãy vẽ 1 góc nhọn x'Oy' có Ox // O'x' , Oy // O'y' . Hãy chứng minh góc xOy và x'Oy' bằng nhau
Nếu đề sửa như vậy thì
Chứng minh
Vẽ đường thẳng OO'
Vì Ox // O'x' nên có hai góc đồng vị bằng nhau :
\(\widehat{O_1}=\widehat{O'}_1\) [1]
Vì Oy // O'y' nên có hai góc đồng vị bằng nhau :
\(\widehat{O_2}=\widehat{O'}_2\) [2]
Từ 1 và 2 suy ra \(\widehat{O_1}-\widehat{O}_2=\widehat{O'}_1-\widehat{O'}_2\)
hay \(\widehat{xOy}=\widehat{x'Oy'}\)
CM
9 tháng 9 2017
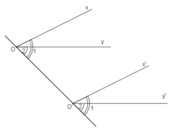
Chứng minh:
Vẽ đường thẳng OO’
Vì Ox // O’x’ nên hai góc đồng vị ∠(O1) và ∠(O'1) bằng nhau
Suy ra: ∠(O1) = ∠(O'1 ) (1)
Vì Oy // O’y’ nên hai góc đồng vị ∠(O2) và ∠(O'2) bằng nhau
Suy ra: ∠(O2) = ∠(O'2)(2)
Từ (1) và (2) suy ra: ∠(O1) - ∠(O2) =∠(O'1) - ∠(O'2)
Vậy ∠(xOy) = ∠(x'O'y')
28 tháng 3 2020
a) Ta có: \(\widehat{x'Oy}=4\widehat{xOz}\)=> \(\widehat{x'Oy}=4.30^0=120^0\)
\(\widehat{x'Oy}+\widehat{yOz}+\widehat{xOz}=180^0\) => \(\widehat{yOz}=180^0-\widehat{xOz}-\widehat{x'Oy}=180^0-120^0-30^0=30^0\)
=> \(\widehat{xOz}=\widehat{yOz}=30^0\)
Oz nằm giữa Ox và Oy
=> Oz là tia p/giác của góc xOy
b) Vì Oz' là tia p/giác của góc x'Oy=>\(\widehat{O_3}=\widehat{O_4}=\frac{\widehat{x'Oy}}{2}=\frac{120^0}{2}=60^0\)
Oy nằm giữa Oz và Oz' nên \(\widehat{zOz'}=\widehat{zOy}+\widehat{yOz'}=30^0+60^0=90^0\)