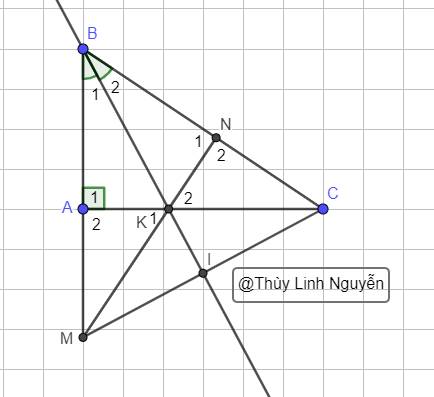
Cho tam giác ABC vuông tại A, trên cạnh BC là điểm G sao cho BM<CM từ điểm kẻ các đường thẳng song song với AC cắt AB tại E, kẻ đường thẳng song song với AB cắt AC tại F
a) Gọi N là điểm đối xứng của điểm M qua AB. Tứ giác AEMF là hình gì?
b) Chứng minh tứ giác AFEN là hình thang cân
c) Tính góc ANB + ACB