Cho đường thẳng
y=mx+(3m-1)
. Tọa độ điểm M cố định mà đường thẳng luôn đi qua là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2019
Giả sử ( x 0 ; y 0 ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.
Ta có:
m x 0 + 3 + (3m - 1) y 0 = 0 với mọi m
⇔ m x 0 + 3 + 3m y 0 - y 0 = 0 với mọi m
⇔ m( x 0 + 3 y 0 ) + 3 - y 0 = 0 với mọi m
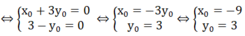
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)
23 tháng 11 2021
\(a,\Leftrightarrow x=0;y=0\Leftrightarrow3m-1=0\Leftrightarrow m=\dfrac{1}{3}\\ b,\text{Gọi điểm cố định mà đt luôn đi qua với mọi m là }A\left(x_0;y_0\right)\\ \Leftrightarrow y_0=mx_0+3m-1\\ \Leftrightarrow m\left(x_0+3\right)-\left(y_0+1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=-3\\y_0=-1\end{matrix}\right.\Leftrightarrow A\left(-3;-1\right)\\ \text{Vậy }A\left(-3;-1\right)\text{ là điểm cố định mà đt đi qua với mọi m}\)
gọi điểm có tọa độ mà đường thăng y=mx+(3m-1) luôn đi qua
là \(M\left(x0,y0\right)\)
=>x0,y0 thỏa mãn y=mx+(3m-1)
\(=>y0=mx0+3m-1\)
\(< =>mx0+3m-1-y0=0\)
\(< =>m\left(x0+3\right)-\left(y0+1\right)=0\)
\(=>\left\{{}\begin{matrix}x0+3=0\\y0+1=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x0=-3\\y0=-1\end{matrix}\right.\)
vậy đường thăng y=mx+(3m-1) luôn đi qua M(-3;-1) cố định
(-3;-1)