Tìm số hạng không chứa x trong khai triển ( 2x3 + \(\dfrac{1}{x^2}\))10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2023
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
N
6 tháng 5 2023
\(C^1_n+C^2_n=15\) (Điều kiện: \(n\ge2\))
\(\Leftrightarrow n+\dfrac{n!}{2!\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)\left(n-2\right)!}{2\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)}{2}=15\)
\(\Leftrightarrow2n+n\left(n-1\right)=30\)
\(\Leftrightarrow2n+n^2-n=30\)
\(\Leftrightarrow n^2+n-30=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=5\\n=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{2}{x^4}\right)^5=C^k_5x^{5-k}\left(\dfrac{2}{x^4}\right)^k=C^k_5x^{5-k-4k}.2^k=C^k_5x^{5-5k}.2^k\)
\(ycbt\Leftrightarrow5-5k=0\Leftrightarrow k=1\)
\(\Rightarrow C^1_5.2^1=10\)
Vậy số hạng không chứa \(x\) trong khai triển là \(10\).
VT
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Là \(\left(x-\dfrac{2}{x}\right)^8\) hay \(\left(x+\dfrac{2}{x}\right)^8\) nhỉ?
13 tháng 11 2021
Ta có:
\(2A_n^2=C_{n-1}^2+C_{n-1}^3\) \(\left(n\ge4\right)\)
\(\Rightarrow2\cdot\dfrac{n!}{\left(n-2\right)!}=\dfrac{\left(n-1\right)!}{2!\left(n-1-2\right)!}+\dfrac{\left(n-1\right)!}{3!\left(n-1-3\right)!}\)
\(\Rightarrow2\cdot n\left(n-1\right)=\dfrac{\left(n-1\right)\left(n-2\right)}{4}+\dfrac{\left(n-1\right)\left(n-2\right)\left(n-3\right)}{6}\)
\(\Rightarrow2n=\dfrac{n-2}{4}+\dfrac{\left(n-2\right)\left(n-3\right)}{6}\)
\(\Rightarrow n=14\) hoặc \(n=0\left(loại\right)\)
Với n=14 ta có khai triển:
\(\left(x^2-\dfrac{1}{x^2}\right)^{14}=\sum\limits^{14}_{k=0}\cdot C_{14}^k\cdot\left(x^2\right)^{14-k}\cdot\left(\dfrac{1}{x^2}\right)^k\)
\(=C_{14}^k\cdot x^{28-4k}\)
Số hạng không chứa x: \(\Rightarrow28-4k=0\Rightarrow k=7\)
Vậy số hạng không chứa x trong khai triển là:
\(C_{14}^7\cdot x^{28-4\cdot7}=C_{14}^7=3432\)
CQ
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
\(\left(x^3-2x^{-1}\right)^8\)
Số hạng tổng quát trong khai triển:
\(C_8^kx^{3k}\left(-2\right)^{8-k}x^{k-8}=C_8^k\left(-2\right)^{8-k}x^{4k-8}\)
Số hạng ko chứa x \(\Rightarrow4k-8=0\Rightarrow k=2\)
Số hạng cần tìm: \(C_8^2.\left(-2\right)^6=...\)
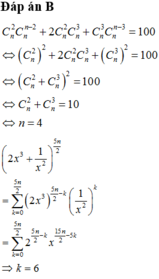
Số hạng tổng quát trong khai triển:
\(C_{10}^k.\left(2x^3\right)^k.\left(x^{-2}\right)^{10-k}=C_{10}^k.2^k.x^{3k}.x^{2k-20}=C_{10}^k.2^k.x^{5k-20}\)
Số hạng không chứa x \(\Rightarrow5k-20=0\Rightarrow k=4\)
Số hạng đó là: \(C_{10}^4.2^4=...\)