GIÚP MIK BÀI 1 TỰ LUẬN VỚI Ạ MIK CẢM ƠN NHÌU Ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.A
2.A
3.B
4.C
5.B
6.C
7.A
8.A
9.B
10.A
11.B
12.A
13.C
14.B
15.B
16.A
17.A
18.A
19.A
20.C

Bài 2:
a: Xét ΔABC có
X là trung điểm của BC
Y là trung điểm của AB
Do đó: XY là đường trung bình
=>XY//AC và XY=AC/2=3,5(cm)
hay XZ//AC và XZ=AC
b: Xét tứ giác AZBX có
Y là trung điểm của AB
Y là trung điểm của ZX
Do đó: AZBX là hình bình hành
mà \(\widehat{AXB}=90^0\)
nên AZBX là hình chữ nhật
d: Xét tứ giác AZXC có
XZ//AC
XZ=AC
Do đó: AZXC là hình bình hành

Bài 5:
a) \(x^2-xy+x-y\)
\(=\left(x^2-xy\right)+\left(x-y\right)\)
\(=x\left(x-y\right)+\left(x-y\right)\)
\(=\left(x+1\right)\left(x-y\right)\)
b) \(xz+yz+4x+4y\)
\(=\left(xz+yz\right)+\left(4x+4y\right)\)
\(=z\left(x+y\right)+4\left(x+y\right)\)
\(=\left(z+4\right)\left(x+y\right)\)
c) \(x^2-x-y^2+y\)
\(=\left(x^2-y^2\right)-\left(x-y\right)\)
\(=\left(x+y\right)\left(x-y\right)-\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-1\right)\)
d) \(x^2+2x+2z-z^2\)
\(=\left(x^2-z^2\right)+\left(2x+2z\right)\)
\(=\left(x+z\right)\left(x-z\right)+2\left(x+z\right)\)
\(=\left(x+z\right)\left(x-z+2\right)\)

Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)

Câu 1: Sống chết mặc bay - Phạm Duy Tốn
Phương thức biểu đạt: tự sự
Câu 2: quan vui vẻ >< dân khổ cực
Câu 1: - Trích từ văn bản Sống chết mặc bay của Phạm Duy Tốn
- PTBĐ chính: Tự sự


\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)





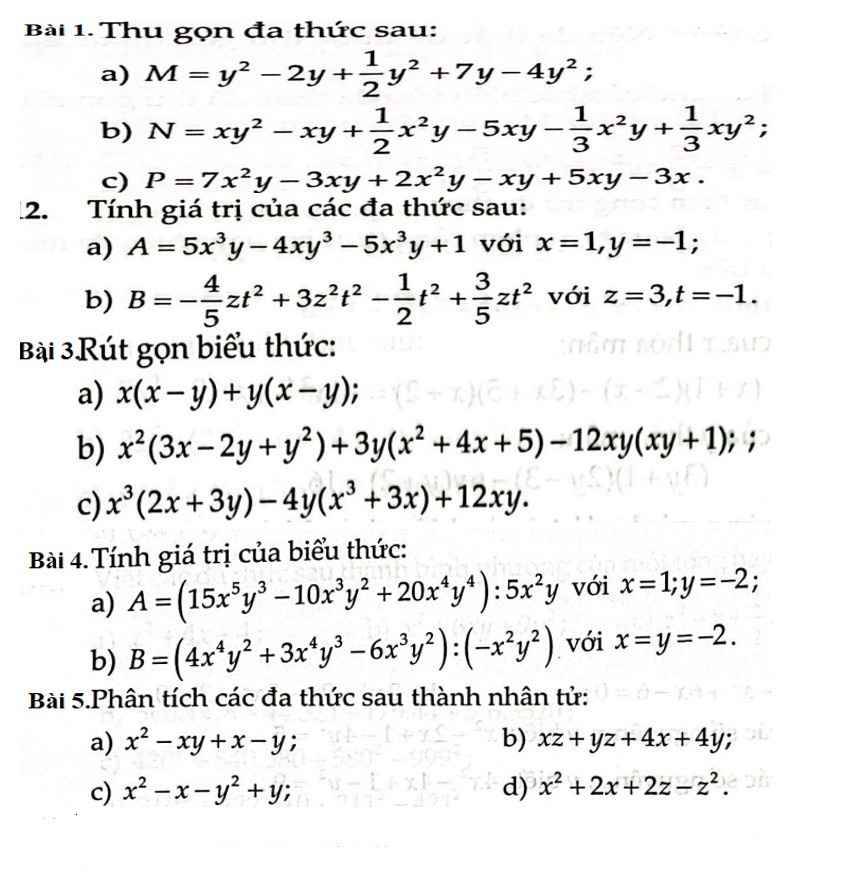


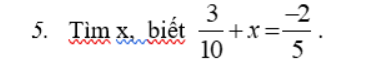 Giúp mik với ạ mik cần gấp lắm cảm ơn nhìu!
Giúp mik với ạ mik cần gấp lắm cảm ơn nhìu!

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)