cho tam giác ABC vuông tại A AB=24 AC=32 Đường trung trực BC cắt AC , BC tại D và E tính DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 7 2018
A B C D E
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
Có \(\widehat{A}\) = \(\widehat{E}\) = 90o
\(\widehat{C}\) chung
=> Tam giác ACB = tam giác ECD (g.g)
=> AC/EC = AB/DE
=> DE = AB.EC/AC = 15cm
Vậy DE = 15cm
16 tháng 9 2023
bạn có thể tham khảo qua link này
https://hoidap247.com/cau-hoi/102853
14 tháng 11 2023
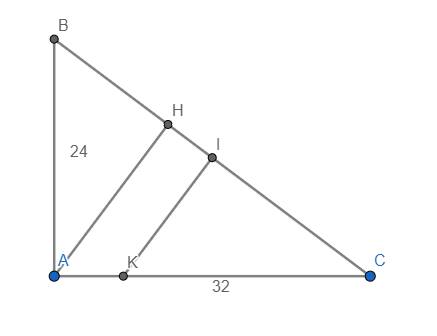
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\))
Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)
Nên \(\widehat{HAC}\approx53,13^o\)
Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm
\(\Rightarrow IB=IC=20cm\)
Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)
Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)
Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)
\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)
Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)
Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)
\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)
12 tháng 3 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=goc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>BA=BE; DA=DE
=>BD là trung trực của AE
19 tháng 2 2022
a. xét tam giác vuông ADE và tam giác vuông ADF,có :
AB = AC ( ABC cân )
Góc EAD = góc FAD ( gt )
AD : cạnh chung
Vậy tam giác vuông ADE = tam giác vuông ADF ( c.g.c )
=> DE = DF ( 2 cạnh tương ứng )
b. xét tam giác vuông BDE và tam giác vuông CDF, có:
góc B = góc C ( ABC cân )
BD = CD ( AD là đường phân giác cũng là đường trung tuyến trong tam giác cân ABC )
Vậy tam giác vuông BDE = tam giác vuông CDF ( cạnh huyền. góc nhọn)
c. ta có: AD là đường phân giác trong tam giác cân ABC cũng là đường trung trực của BC
19 tháng 2 2022
a: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)
Do đó: ΔAED=ΔAFD
SUy ra: DE=DF
b: Xét ΔBDE vuông tại E và ΔCDF vuông tại F có
BD=CD
DE=DF
Do đó: ΔBDE=ΔCDF
c: Ta có: ΔABC cân tại A
mà AD là phân giác
nên AD là đường trung trực của BC
pytago \(=>BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40cm\)
vì ED là trung trực của BC \(=>EB=EC=\dfrac{1}{2}BC=20cm\)
vì ED................................\(=>\angle\left(DEC\right)=90^o\)
mà tam giác ABC vuông tại A \(=>\angle\left(A\right)=90^o\)
\(=>\angle\left(DEC\right)=\angle\left(A\right)=90^o\)
có \(\angle\left(C\right)chung\)\(=>\Delta DEC\sim\Delta BAC\left(g.g\right)\)
\(=>\dfrac{EC}{AC}=\dfrac{ED}{AB}=>\dfrac{20}{32}=\dfrac{ED}{24}=>ED=15cm\)
gửi bạn