Tam giác ABC có phương trình các cạnh là AB: 4x + 3y - 1 = 0, AC: 3x + 4y = 6, BC: y = 0. Tâm I của đường tròn nội tiếp tam giác ABC có hoành độ là ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bằng việc lần lượt giải các hệ phương trình bậc nhất hai ẩn, ta có tọa độ các đỉnh của tam giác là A − 4 7 ; 16 7 , B − 10 11 ; 14 11 , C − 8 ; 6 .
Ta có công thức tính diện tích tam giác ABC là: S = 1 2 . d A , B C . B C = 1 2 2. − 4 7 + 3. 16 7 − 2 13 . − 8 + 10 11 2 + 6 − 14 11 2 = 338 77
Đáp án là phương án C.

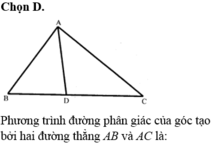




Cách làm
1. Từ phương trình 3 cạnh suy ra tọa độ 3 đỉnh của tam giác
2. Gọi D là chân đường phân giác trong góc A của ΔABC ⇒ \(\overrightarrow{BD}=\dfrac{AB}{AC}.\overrightarrow{DC}\)
3. Tâm đường tròn ngoại tiếp I của tam giác ABC là chân đường phân giác trong góc B của ΔABD