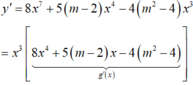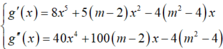Bài 1: Có tất cả bao nhiêu giá trị của m nguyên để hàm số:
y = x8 + (m - 2)x5 - (m2 - 4)x4 + 1 đạt cực tiểu tại x = 0?
(Mã đề 123, đề thi năm 2018).
Bài giải:
Với đề thi THPT quốc gia môn Toán, đây là một trong những câu khó. Không nhiều các bạn học sinh giải được đề toán trên. Đây là một hàm số bậc 8, hoàn toàn khác với những hàm số thông dụng được học trên lớp, để giải được bài này, các bạn cần phải sử dụng kiến thức từ định nghĩa và tính chất của cực trị hàm số bất kì. Ta có:
y' = 8x7 + 5(m - 2)x4 - 4(m2 - 4)x3 + 1
Hàm đạt cực tiểu tại x = 0 thì y'(x) = 0 và y'(x) đổi dấu từ âm sang dương khi x chạy qua điểm 0. Từ đó ta tương đương với số hạng chứa x có lũy thừa thấp nhất có hệ số khác 0 trong biểu thức y’ là lũy thừa bậc lẻ, hệ số dương.
Có nghĩa là :
–4(m2 - 4) > 0 và m - 2 = m² – 4 = 0
⇔ –2 < m < 2 hoặc m = 2
⇒ m = {-1, 0, 1, 2 }
Tóm lại ta nhận được 4 giá trị của m là số nguyên của m để hàm số đạt cực tiểu tại x = 0.
Bạn đọc có thể nhận thấy không hề đơn giản chút nào để giải được bài tập tìm cực trị hàm số trên. Vì thế chúng ta hãy cùng luyện tập thật nhiều và chắc các dạng bài cực trị trên. Từ đó với kĩ năng và kiến thức trên các em mới giải nhanh được câu hỏi tương tự.
giúp mik vs